电机学
第一章 绪论
电与磁的转换是电机学中最重要的部分之一。
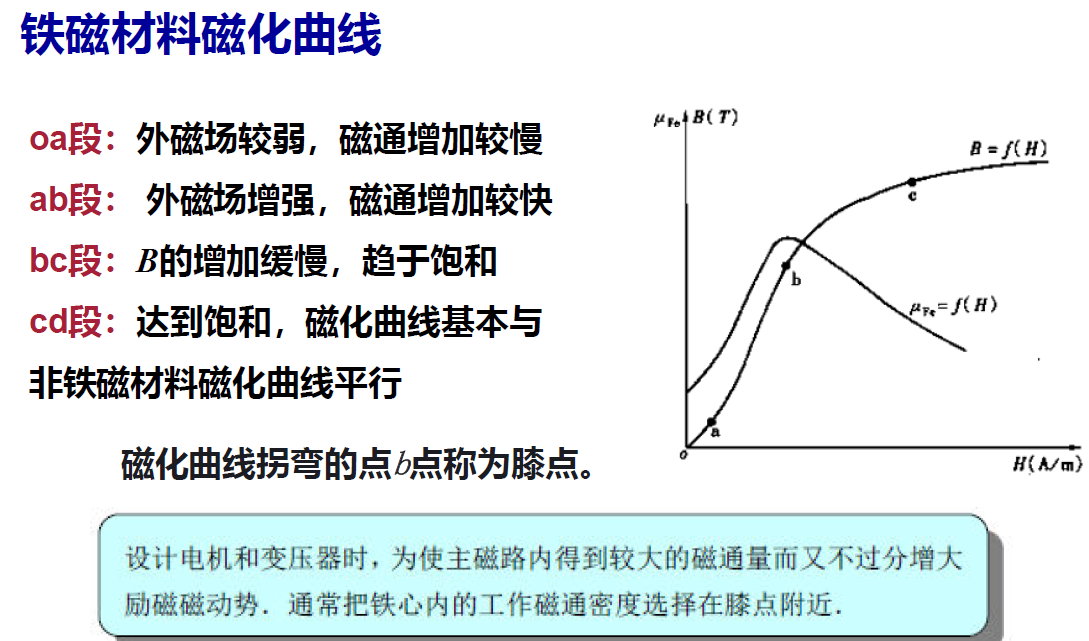
b点为膝点,变压器一般都会工作在膝点附近。
电机的分类:
旋转电机的转速为 $n=\frac{60f}{p}$,其中 $p$ 为极对数。
磁阻、磁导的计算:
可以得到磁阻 $R_\mathrm{m}=\frac{l}{\mu A}$ 或磁导 $\Lambda=\frac{\mu A}{l}$。
电感的计算:
第二章 变压器
复习:变压器的基本公式
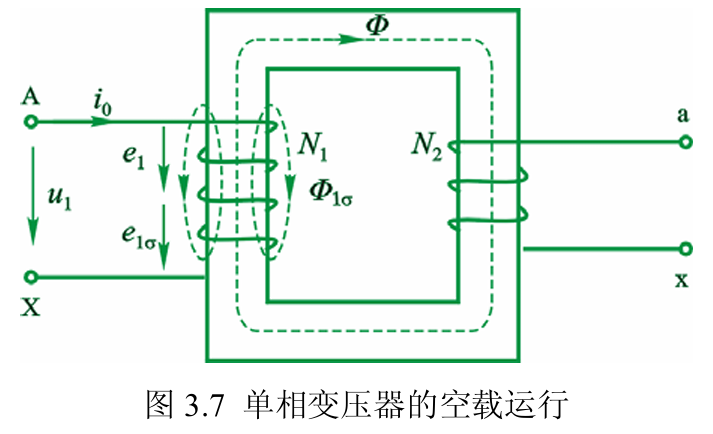
空载运行
可见一次侧有主磁通和漏磁通,二次侧由于电流为零只有主磁通。
变压器中主磁通与漏磁通的区别:
| 主磁通 | 漏磁通 | |
|---|---|---|
| 磁路 | 铁芯 | 非铁磁材料 |
| 磁阻 | 小 | 大 |
| 数量 | >99% | <1% |
| 交链绕组 | 一次和二次 | 一次或二次 |
| 功能 | 传递能量 | 感应漏电动势 |
| 与产生它的电流关系 | 非线性 | 线性( $\mu$ 不变) |
| 产生的电感是否变化 | 变化 | 不变 |
感应电动势的计算:
设 $\varPhi=\varPhi_\mathrm{m} \cos{\omega t}$,则有
其有效值为
相量形式为
务必牢记 $U_1\approx E_1=4.44fN\varPhi_\mathrm{m}$ !!!
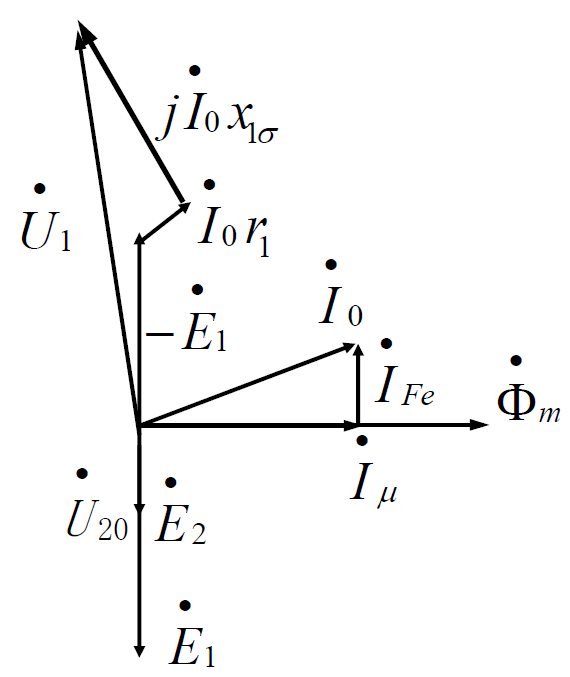
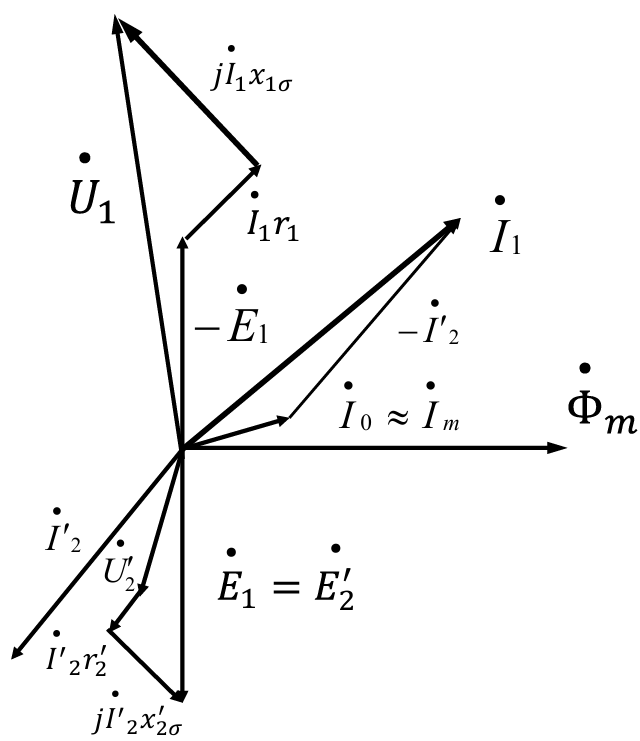
空载相量图:
空载电流:
分为两部分:励磁电流和铁耗电流,其中励磁电流远大于铁耗电流。
铁耗的经验公式:$p_{_\mathrm{Fe}}=C_{_\mathrm{Fe}}f^{1.3}B^2V$ 。
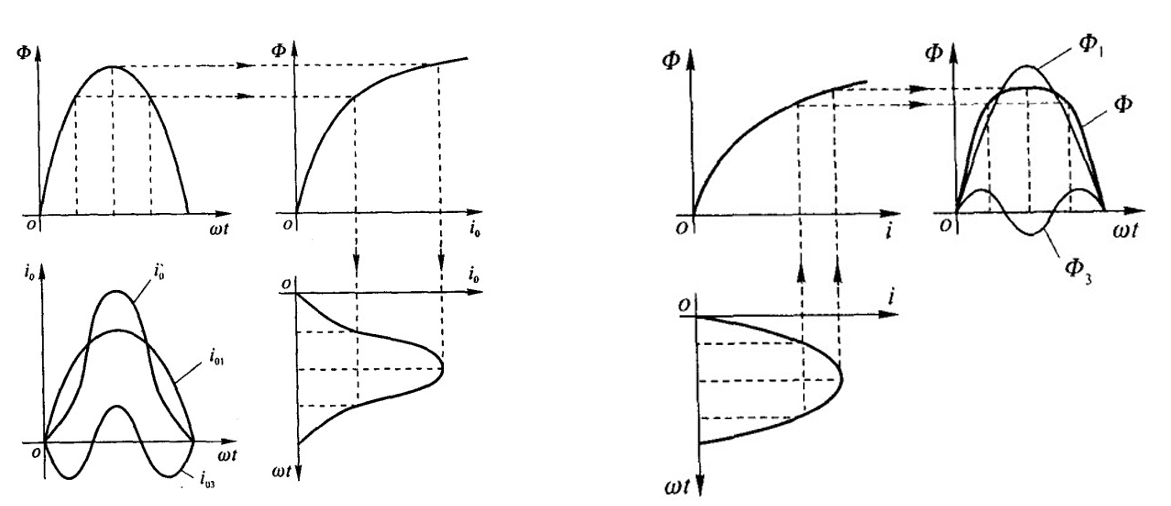
在磁路饱和时,电流、磁通和电势波形如下:
当 $i_0$ 为尖顶波时,$\varPhi$ 和 $e$ 都是正弦波;当 $i_0$ 为正弦波时,$\varPhi$ 为平顶波、 $e$ 为尖顶波。
于是我们就可以把励磁支路等效为一个电阻和一个电感。
负载运行
电路方程
为了方便计算,我们将二次侧电路量折算到一次侧。由于是折算,所以折算后的值并非实际值!
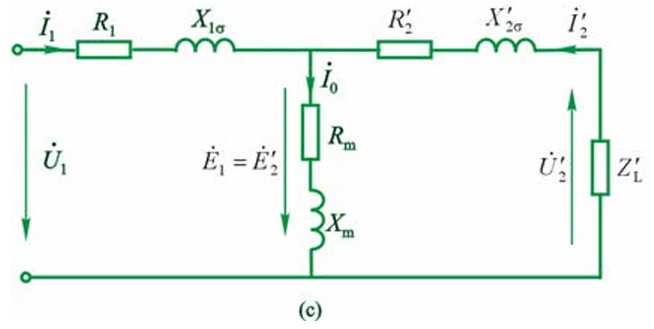
由此,我们可以得出变压器的 T 形等效电路。
当然,激进一些,我们可以将 T 形等效进一步简化为 $\Gamma$ 形等效电路,即把励磁支路移到最左边。
更激进一些,我们直接断开励磁支路,称为简化等效电路。
参数测定
空载试验测励磁
高压侧开路,在低压侧加电压,这样可以避免加入高电压,保证安全。
由于 $Z_\mathrm{m} \gg Z_1$,可以忽略 $Z_1$,即认为空载试验测量的就是励磁支路的电压电流。
这里是在低压侧测得的数据,需要折算到高压侧。
空载试验不可以回头测量,因为磁化路径不一致。
短路试验测绕组
低压侧短路,在高压侧加电流,这样可以避免加入大电流,保证安全。
同理,由于 $Z_\mathrm{m} \gg Z_k$ ,可以忽略励磁支路,即认为短路试验测量的就是绕组的电压电流。电阻的测量结果可能需要折算至 $75^\circ \mathrm{C}$ 。
折算公式为 $r_{k, 75}=\displaystyle\frac{234.5+75}{234.5+\theta}r_{k, \theta}$。
这里测出来的电压电流是两个绕组的,不能单测某一侧。
标幺值
如果使用了标幺制,那么二次侧就不需要折算了,直接在等效电路中计算即可。
一般都会选取电压和电流作为基准量。
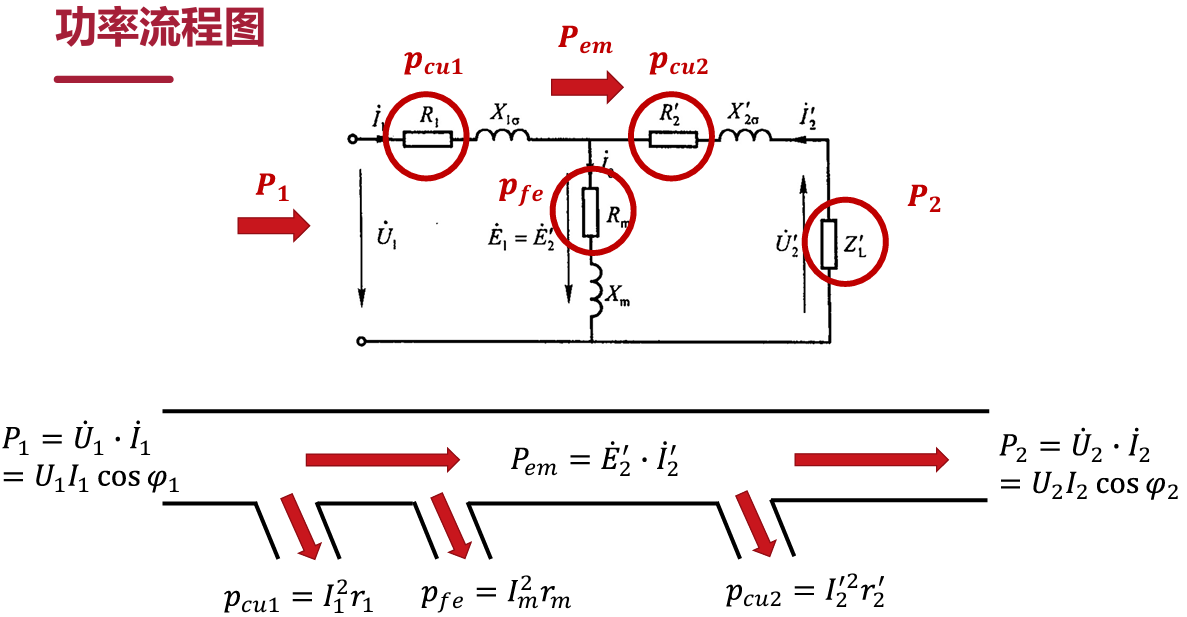
功率流程图
会画就行了。
运行特性
运行特性主要需要了解两部分:电压调整率(电压变化率)和效率。
这一部分需要定义两个量:负载系数 $\beta=\frac{I_2}{I_\mathrm{2N}}=I_2^*$ 和相数 $m$ (一般为3)。
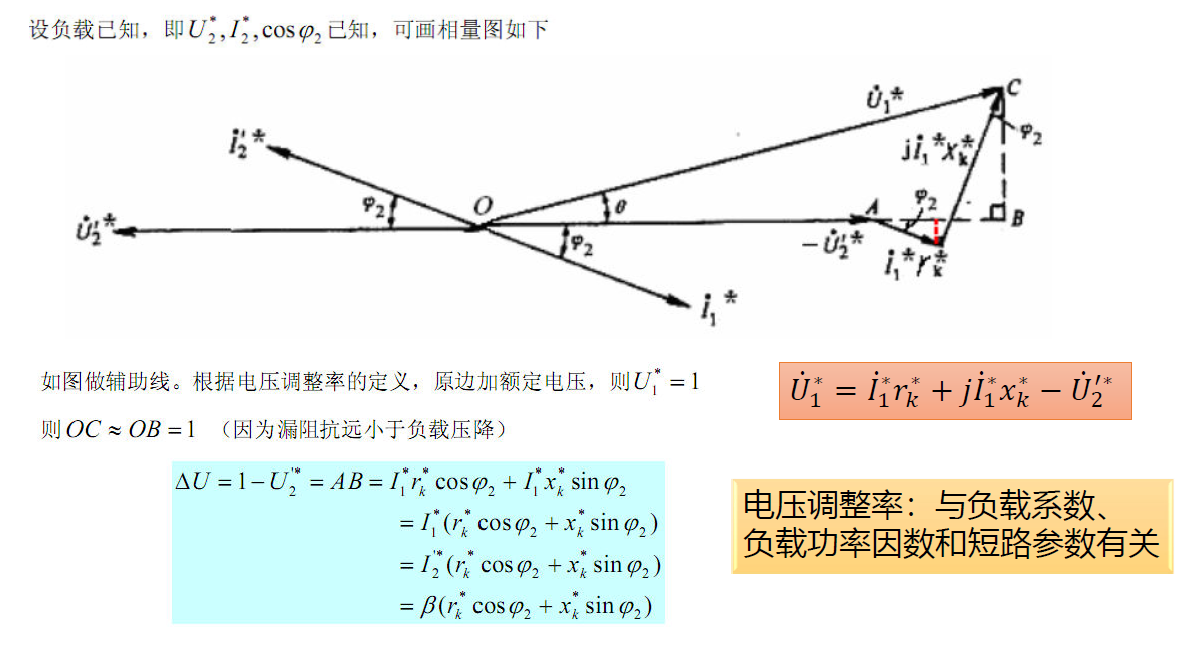
在推导电压调整率的时候,我们使用标幺制,并且忽略了励磁支路的影响,即认为 $I_1=-I_2’$ , $\dot{U}_1=\dot{I}_1 r_\mathrm{k} + \mathrm{j}\dot{I}_1 x_\mathrm{k} + \dot{U}_2’$。
电压调整率:
其反映了变压器供电的稳定性。
通过相量图,我们可以得到电压调整率的近似计算式:
效率:
变压器的损耗 $\Sigma P$ 包括铜耗和铁耗。
为了减少涡流损耗,铁芯一般用硅钢片叠成。硅和片用于增加电阻,减小电流;钢用于减小磁阻。
计算损耗用等效电路上的电阻计算,即
那么对于短路试验,如果我们将二次侧电压近似看成额定电压,则有
对于空载试验,有
负载上的功率有
综合上述三式,可以得到效率
若不加以说明,则效率指 $\beta=1$ 时的额定效率;当 $\beta=\sqrt{\frac{p_0}{p_{\scriptscriptstyle\mathrm{kN}}}}$ (即铁耗与铜耗相等)时效率最大。
三相变压器
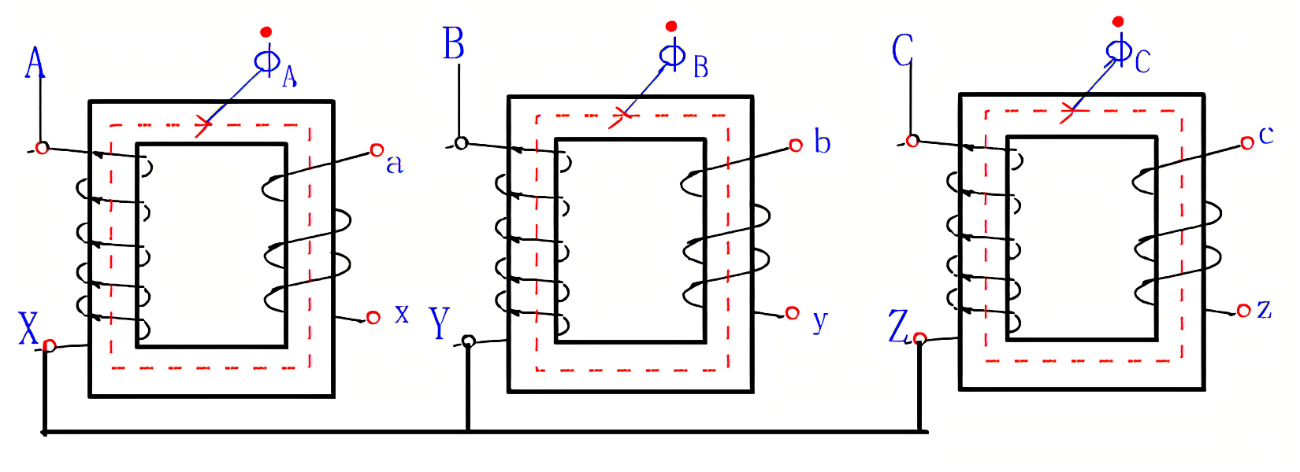
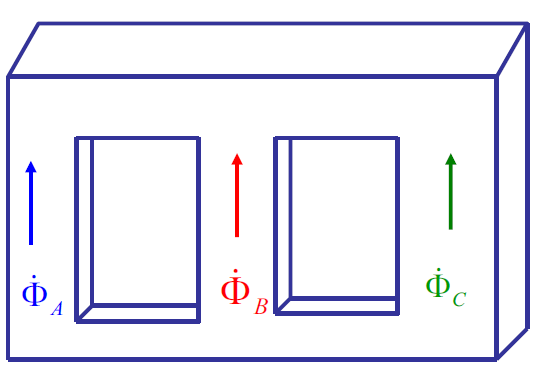
在结构上,分为组式和心式。
组式三相变压器的磁路彼此独立。
心式三相变压器的 B 相磁路与 A、C 两相不同,空载时电流不均衡。
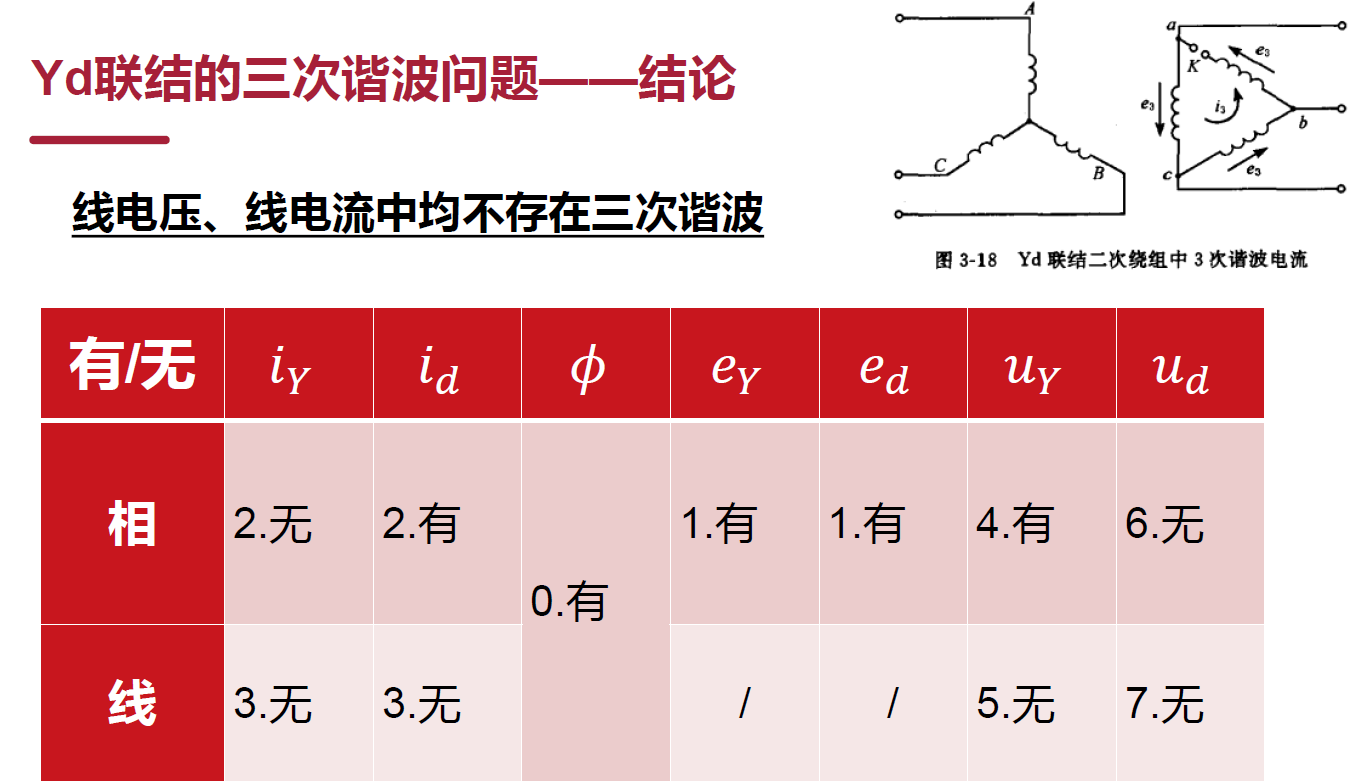
三相变压器的三次谐波问题:
结论:线电压和线电流中均不会含有三次谐波。
第三章 交流电机绕组基本理论
开始之前,先定义一些名词。
电角度
将电机剖开,横截面是一个圆,其几何角度(机械角度)为 $360^\circ$。
从电磁的角度来看,一对 N、S 极旋转一圈构成了一个磁场的周期,即一对极应该对应 $360^\circ$ 电角度。
那么应该有其中 $\Omega$ 为机械角度,$\omega$ 为电角度,$p$ 为极对数。
频率
若电机有 $p$ 对极,则转子旋转一周,感应电势 $e$ 交变 $p$ 次,得到频率为
其中 $n$ 为转速(rpm)。
槽距(电)角
相邻两槽之间相距的电角度称为槽距(电)角。
其中 $Z$ 为槽数。
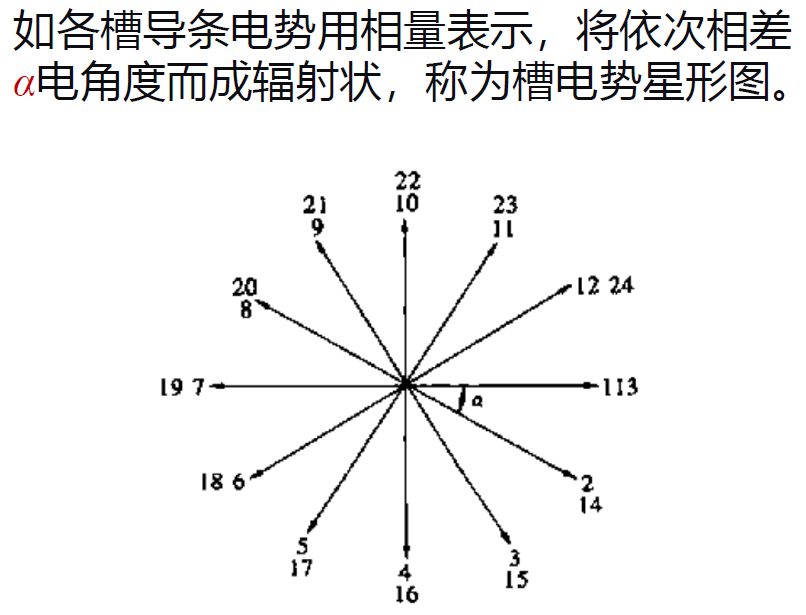
槽电势星形图
相带
每组绕组在电枢圆周上连续占据的电角度称为相带。
采用 $60^\circ$ 相带可以获得较大的基波电势。每极每相槽数
整个电机定子中每相在每个极下所占有的槽数称为每极每相槽数。
极距
相邻两个磁极轴线间,沿定子铁芯内表面的圆弧长度称为极距。
有两种表示方法,第一种为圆弧长度表示法,不常用;第二种为槽数表示法节距
一个线圈的两边在定子圆周上所跨的距离称为节距。
当 $y=\tau$ 时,称为整距;当 $y<\tau$ 时,称为短距;当 $y>\tau$ 时,称为长距。
一般单层绕组用整距,双层绕组用短距。
单层叠绕组展开图的绘制
计算每极每相槽数和槽距角,绘制槽电势星形图和相带,然后展开即可。
正弦分布磁场下的绕组电动势
从最小单位入手,慢慢叠加,最后求得每相的电动势。
导体电动势
当 $p$ 对极的正弦磁场以转速 $n_1$ 切割导体时,电动势有效值为
其中 $B_\mathrm{m1}$ 为正弦波磁感应强度幅值,$v=2p\tau\frac{n_1}{60}$,节距以长度计。
频率为 $f=\frac{np}{60}$,磁链为 $\varPhi_1=\frac{2}{\pi}B_\mathrm{m1}\tau l$,代入有
匝电动势
若导体 $c_1$ 与 $c_2$ 之间相差 $y_1$ 槽,则 $E_\mathrm{c2}$ 滞后 $E_\mathrm{c1}$ 一个电角度 $y_1\alpha_1$。
线圈电动势为 $ \dot{E}_\mathrm{t1}=\dot{E}_\mathrm{c1}-\dot{E}_\mathrm{c2}=2E_\mathrm{c1}\displaystyle\sin{\frac{y_1}{\tau}\frac{\pi}{2}} $。
定义短距系数 $k_\mathrm{y1}=\displaystyle\sin{\frac{y_1}{\tau}\frac{\pi}{2}}$,则有
线圈组电动势
每个线圈组由 $q$ 个线圈组成,每个线圈相差 $\alpha_1$ 电角度,则有
其模值为
定义分布系数 $k_\mathrm{q1}=\displaystyle\frac{\sin{\frac{q\alpha_1}{2}}}{q\sin{\frac{\alpha_1}{2}}}$,则有
绕组系数 $k_{\scriptscriptstyle\mathrm{N1}}=k_\mathrm{q1}k_\mathrm{y1}$。
相电动势
每相绕组有 $a\hspace{0.5em} (a\le2p)$ 条并联支路,每条支路由 $c$ 个极相组串联而成,则
记每相有效串联匝数 $N=cqN_\mathrm{c}$,则有 $E_{\varphi1}=4.44Nf\varPhi_1k_{\scriptscriptstyle\mathrm{N1}}$,$N$ 亦可用 $N=\frac{\text{整个电机绕组总匝数}}{3a}$ 来计算。
非正弦磁场高次谐波和处理方法
在气隙中,由于磁路高度饱和,磁场一般呈平顶波,其谐波次数 $\nu=3,5,7,\cdots$
此时,$\nu$ 次谐波极对数 $p_\nu=\nu p$,极距 $\tau_\nu=\displaystyle\frac{\tau}{\nu}$,转速 $n_\nu=n_1$,频率 $f_\nu=\nu f_1$,电动势 $E_{\varphi\nu}=4.44Nf_\nu \varPhi_\nu k_{\scriptscriptstyle\mathrm{N}\nu}$。
其中,$k_{\scriptscriptstyle\mathrm{N}\nu}=k_{y\nu}k_{q\nu}$,$k_{y\nu}=\sin{\left(\frac{\pi}{2}\cdot\frac{\nu y_1}{\tau}\right)}$,$k_{q\nu}=\displaystyle{\frac{\sin{\frac{q\cdot\nu\alpha_1}{2}}}{q\sin{\frac{\nu\alpha_1}{2}}}}$。
削弱谐波电动势的方法:
- 使气隙中磁场分布尽可能接近正弦波
采用对称三相绕组
多采用星形接法以避免环流
采用短距绕组
使 $k_{y\nu}=\sin{\left(\frac{\pi}{2}\cdot\frac{\nu y_1}{\tau}\right)}=0$ 即可。
此时 $y_1=\left(1-\frac{1}{\nu}\right)\tau$,即比整距短 $\frac{1}{\nu}\tau$。有时也会取 $\nu=6$ 以同时削减 5、7 次谐波。
采用分布绕组
使 $k_{q\nu}=\displaystyle{\frac{\sin{\frac{q\cdot\nu\alpha_1}{2}}}{q\sin{\frac{\nu\alpha_1}{2}}}}$ 减小,这时增大 $q$ 即可。
一般会取 $2\le q\le 6$。
谐波磁动势
这一部分推导复杂,直接记结论。
- $3k$ 次谐波不存在
- $6k-1$ 次谐波,转速为 $\frac{1}{6k-1}n_1$,方向与基波相反
- $6k+1$ 次谐波,转速为 $\frac{1}{6k+1}n_1$,方向与基波相同
第四章 异步电机
同样,在开始之前,定义一些概念。
同步转速
定子磁场旋转的速度。
转差率
其中 $n$ 为转子的实际转速。
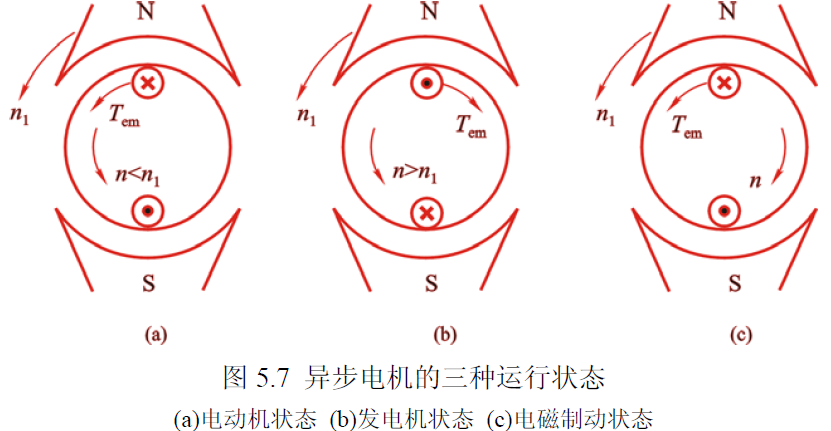
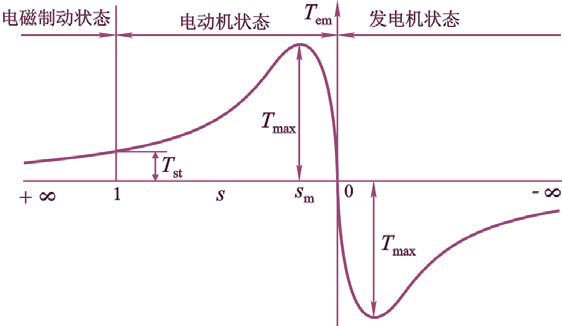
三种工作状态
处于电动机状态时,$0{<}n{<}n_1$,$0{<}s{<}1$;
处于发电机状态时,$n>n_1$,$s<0$;
处于电动机状态时,$n<0$,$s>1$。
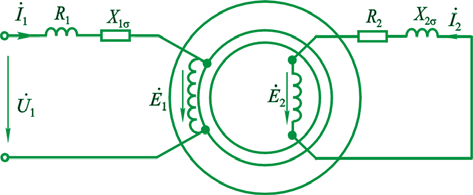
转子静止时的等效电路
通过磁势推导出电动势变比
电流变比
绕线式转子的相数与定子相数相等;鼠笼形转子的相数 $m_2=Z_2$,$Z_2$ 为转子导条数,绕组系数为1。
后面的研究默认使用绕线式异步电机。
转子旋转时的等效电路
转子中电动势的频率为 $f_2=\displaystyle\frac{(n_1-n)p}{60}=sf_1$,
电动势有效值为 $E_{2s}=4.44f_2N_2k_{\scriptscriptstyle\mathrm{N2}}\varPhi_\mathrm{m}=sE_2$。
正常运行时,转子电动势频率很小,铁耗很低。
由于正常运行时定转子频率不同,需要进行折算,我们用一个静止的转子来替代旋转的转子。
转差率为 $s$ 时
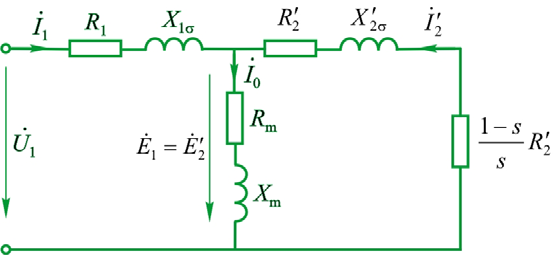
这意味着,我们只需要在转子回路中把负载变为一个大小为 $\displaystyle\frac{1-s}{s}R_2$ 的电阻即可。于是我们得到了等效电路:
与变压器相同,我们仍可以把励磁支路直接平移到一次侧。
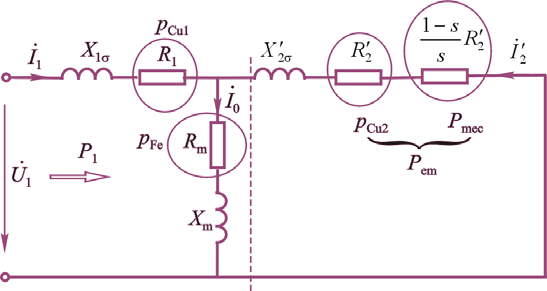
功率、转矩平衡方程
输入功率
定子铜耗
铁耗
定子给转子传递的电磁功率
转子铜耗
剩下的就是机械功率
扣除机械损耗和附加损耗后,就是机械输出功率
电磁转矩
其中 $\Omega=\frac{2\pi n}{60}=\frac{2\pi(1-s)n_1}{60}=(1-s)\Omega_1$,$\Omega_1$ 为同步角速度。
输出转矩和空载转矩的计算,用 $P_2$ 和 $p_\mathrm{mec}+p_\mathrm{ad}$ 除以机械角速度即可。
对于电磁转矩还有个结论
电磁转矩的三种表达式
牢记机械角速度 $\Omega=\frac{2\pi n}{60}=\frac{2\pi f}{p}$
物理表达式:
而 $E_2’=4.44f_1N_1k_{\scriptscriptstyle\mathrm{N1}}\varPhi_\mathrm{m}$,代入后有
其中 $C_{\scriptscriptstyle\mathrm{M}}=\displaystyle\frac{pm_2N_2k_{\scriptscriptstyle\mathrm{N2}}}{\sqrt{2}}$ 是一个常数。
这个式子就与直流电机的转矩表达式统一了。
参数表达式:
转子电流
电磁功率
在 $U_1$ 和 $f_1$ 为常数时,可以认为电磁转矩仅和转差率有关。
对转矩表达式求导,得到临界转差率和对应的最大转矩
由于 $R_1$ 非常小,可以忽略,则有
求起动转矩:
把 $s=1$ 代入即可。如果要起动转矩最大,则让 $s_\mathrm{m}=1$ 即可,此时转子回路电阻满足 $R_2’+R_\mathrm{st}’=X_{1\sigma}+X_{2\sigma}’$。
实用表达式:
求最大电磁转矩时,我们顺便知道了 $X_{1\sigma}+X_{2\sigma}’=\frac{R_2’}{s_\mathrm{m}}$,可以把最大电磁转矩和电磁转矩改写为
二者相除,有
异步电机的起动
直接起动时,由于转差率为1,短路阻抗很小,起动电流非常大,需要使用一些其他的起动方式。
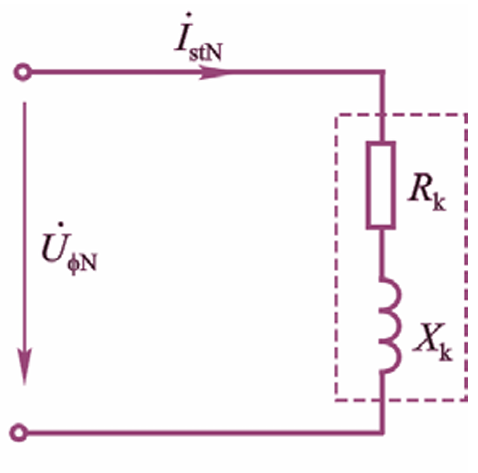
直接起动
适用于小容量、轻载的工况($P_\mathrm{N}\le 7.5 \mathrm{kW}$)。
降压起动
适用于大容量、轻载的工况($P_\mathrm{N}\ge 20 \mathrm{kW}$)。
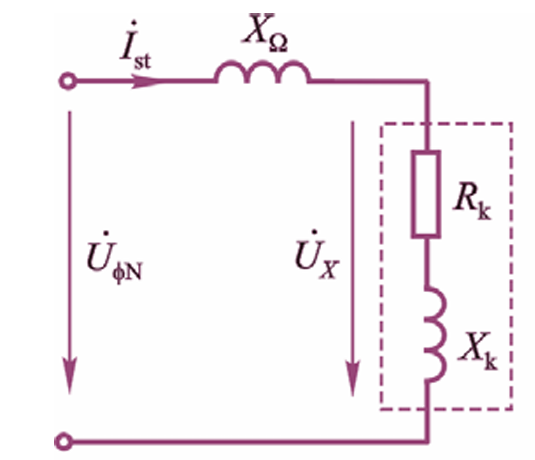
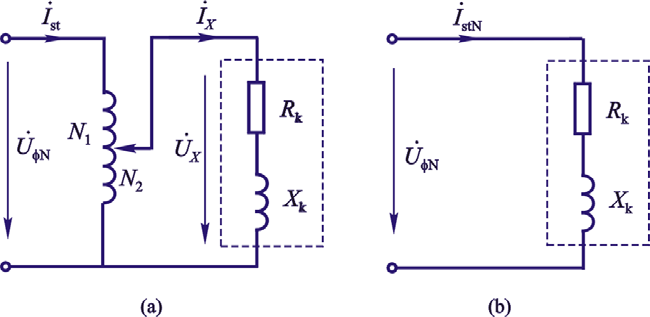
定子串电抗降压起动
这会让电阻上的能耗非常大。
若$\frac{I_\mathrm{st}}{I_\mathrm{stN}}=\frac{U_\mathrm{x}}{U_\mathrm{\varphi N}}=\frac{1}{a}$,则有
此时阻抗满足
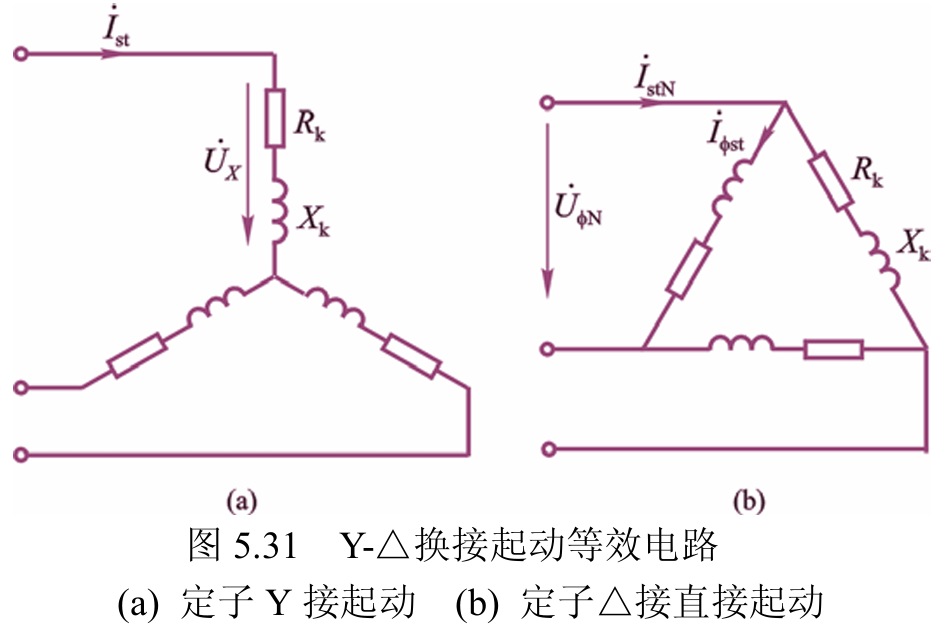
使用星三角起动器
只有正常运行时定子绕组为三角形接法,且三相绕组首尾六个端子全部引出时才能使用。
则对于每一相有
那对于电网
转矩也为额定转矩的 $\frac{1}{3}$。
自耦变压器起动
电压和电流满足 $\frac{U_\mathrm{x}}{U_\mathrm{\varphi N}}=\frac{1}{a}$,$\frac{I_\mathrm{x}}{I_\mathrm{stN}}=\frac{1}{a}$,又由变压器公式 $U_\mathrm{\varphi N}I_\mathrm{st}=U_\mathrm{x}I_\mathrm{x}$,得到
异步电机的调速
异步电机的调速,按照转差功率 $P_s=sP_\mathrm{em}$ 的不同分为三类
转差功率消耗型
调压调速、滑差离合器调速和转子串电阻调速都属于这类。
转差功率回馈型
串级调速属于这类,即在转子中串入一个可变电动势以回馈电网。
转差功率不变型
变极调速和变频调速属于这一类,也是应用最为广泛的一类。
第五章 同步电机
电枢反应
在有负载时,气隙磁场会由励磁电流和电枢电流共同建立,二者共同影响磁场。
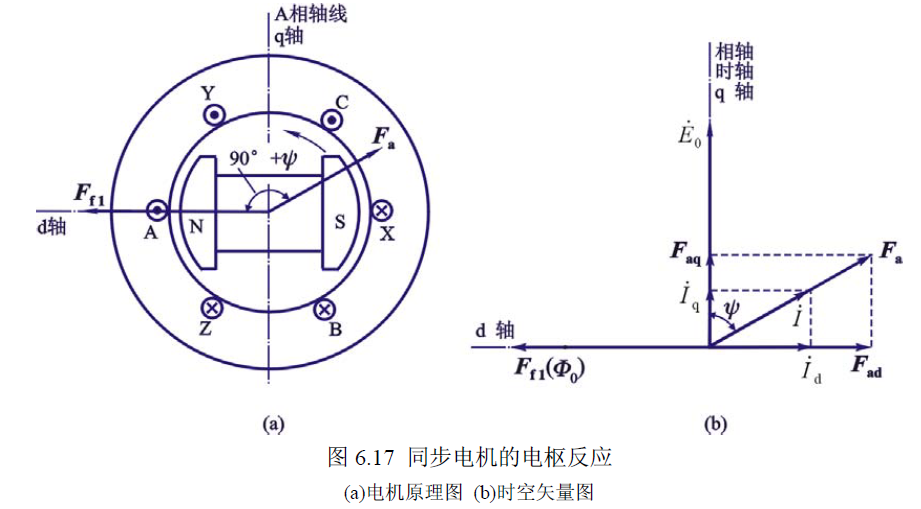
我们假设极对数 $p=1$,记沿磁极方向的坐标轴为直轴(d轴),垂直磁极方向的坐标轴为交轴(q轴),直轴超前交轴 $90^\circ$。
相量图中,定义三个角度:
三个角度满足 $\psi=\varphi+\delta$。
交轴电枢反应与机电能量转换有关,直轴与磁场的建立有关。
隐极机电枢反应
隐极同步电机气隙均匀,可以认为同一电枢电动势在气隙任何位置产生的磁通相同。
凸极机电枢反应
凸极同步电机气隙不均匀,我们可以将电枢磁动势正交分解到直轴和交轴以进行分析。
隐极同步电机的负载运行
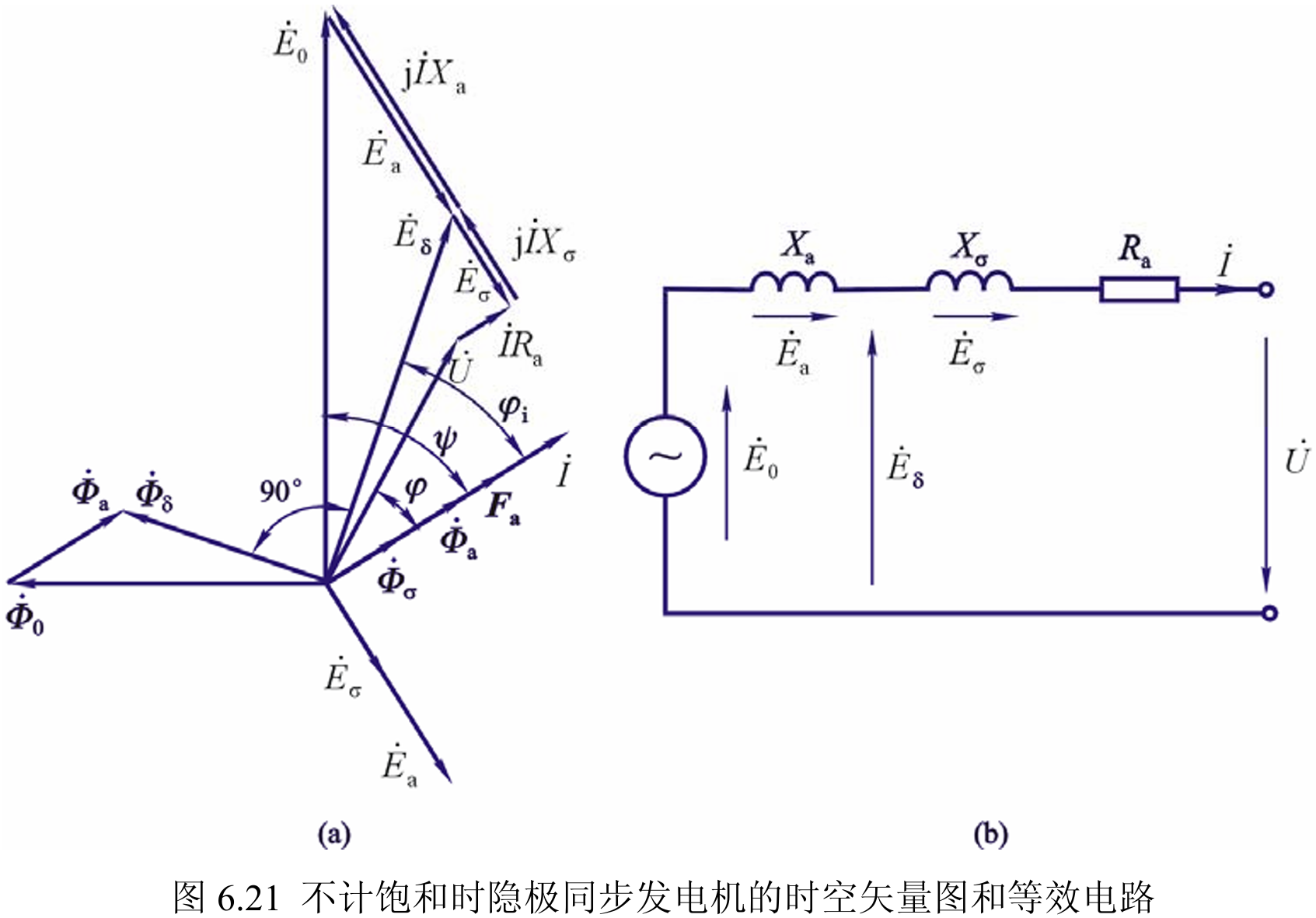
在不饱和时:
图中 $X_\mathrm{a}$ 为电枢反应电抗,$X_\sigma$ 为漏电抗。记同步电抗 $X_\mathrm{t}=X_\mathrm{a}+X_\sigma$ (不过为了与凸极机统一,都用 $X_\mathrm{d}$ 表示同步电抗了)。
励磁电动势电动势和机端电压满足关系
凸极同步电机的负载运行
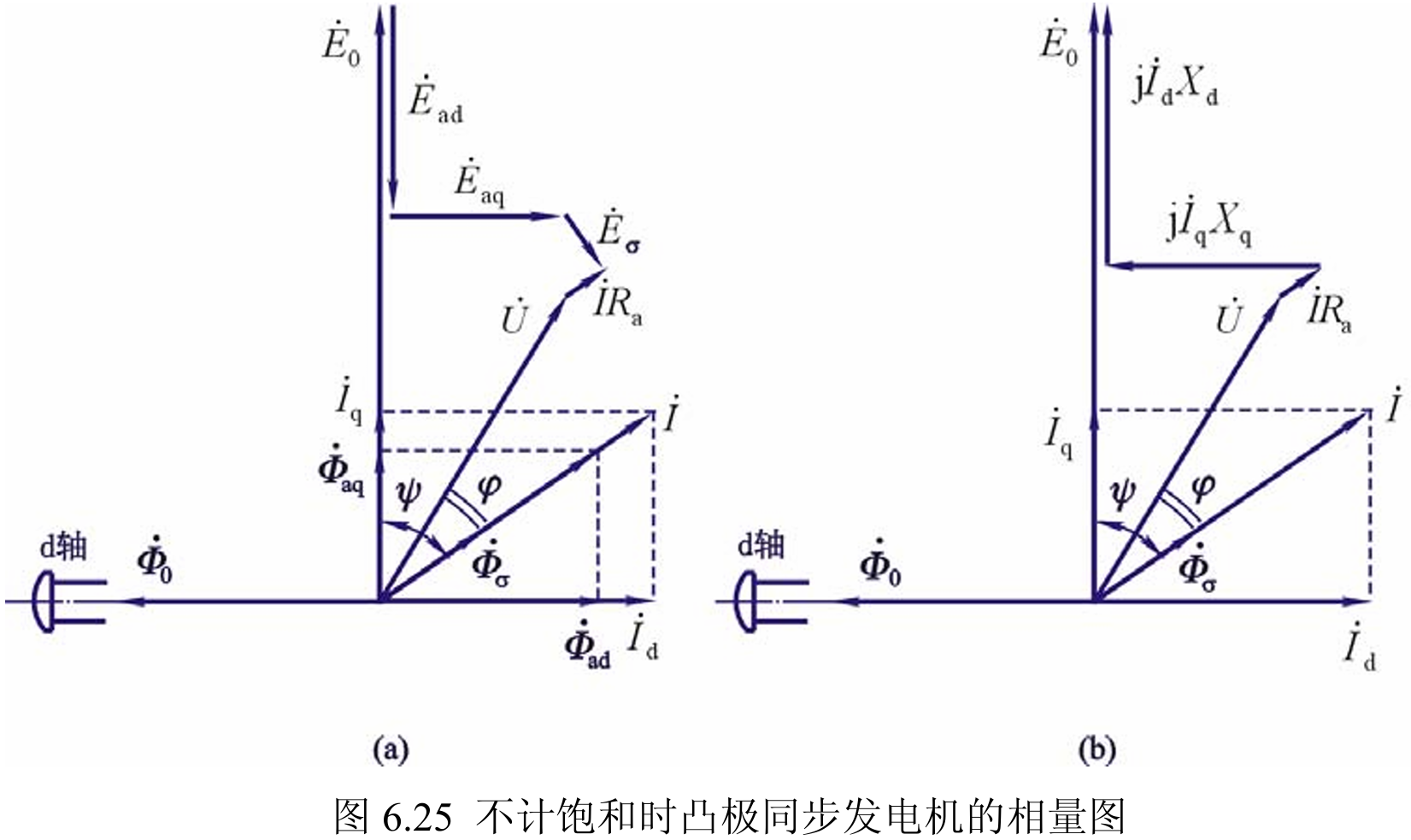
在不饱和时:
同样,记直轴同步电抗 $X_\mathrm{d}=X_\mathrm{ad}+X_\sigma$,交轴同步电抗 $X_\mathrm{q}=X_\mathrm{aq}+X_\sigma$。
励磁电动势和机端电压满足
在相量图上可以得到
运行特性
这一部分的图用的都是标幺值。
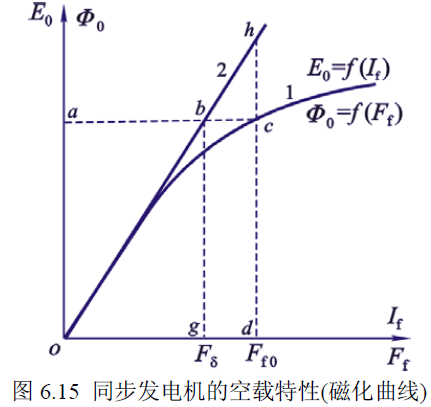
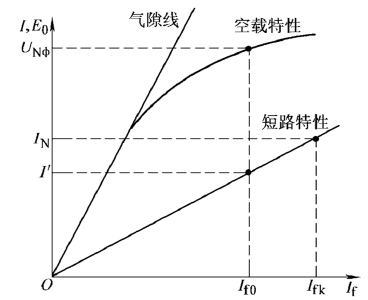
空载特性
图像为 $n=n_{\scriptscriptstyle\mathrm{N}}$, $I=0$ 时,$U_0=E_0=f(I_f)$ 的图像。
在不饱和时,$E_0^{*}=\varPhi_0^{*}$;饱和后,当 $E_0^{*}=\varPhi_0^{*}$ 时,二者对应的励磁电流不同。
定义气隙线为直线 $\overline{oh}$,饱和系数为 $k_\mu=\displaystyle\frac{\overline{hd}}{\overline{bg}}=\frac{E_0’}{U_N}$。
这说明在饱和时,产生相同的磁通所需要的磁动势是不饱和时的 $k_\mu$ 倍。由于电机中有剩磁,测出来的图像需要先按照气隙线延长,然后向右平移,以校正空载特性曲线。
过饱和会导致电机用铜多,电压调节困难;饱和度太低会导致电压变化率大,铁心利用率低。
短路特性
图像为 $n=n_{\scriptscriptstyle\mathrm{N}}$, $U=0$ 时,$I_k=f(I_f)$ 的图像。
图像就是一条过原点的直线,因为气隙不饱和,短路电流起去磁作用。
此时,$\dot{E}_\delta=\dot{U}+\dot{I}R_\mathrm{a}+\mathrm{j}\dot{I}X_\sigma \approx \mathrm{j}\dot{I}X_\sigma$
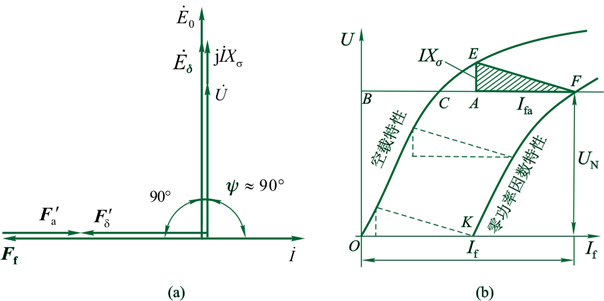
零功率因数负载特性
图像为 $n=n_{\scriptscriptstyle\mathrm{N}}$, $I=Const$, $\cos\varphi=0$ 时,$U=f(I_f)$ 的图像。
$\dot{E}_0=\dot{U}+\dot{I}R_\mathrm{a}+\mathrm{j}\dot{I}X_\mathrm{t}\approx \mathrm{j}\dot{I}X_\mathrm{L} + \mathrm{j}\dot{I}X_\mathrm{t}$
就是在机端接了个电感。
图中 CA 为克服漏电抗的励磁电流。
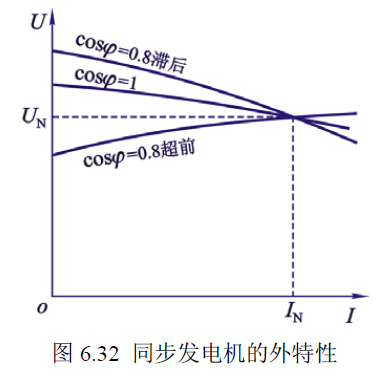
外特性
图像为 $n=n_{\scriptscriptstyle\mathrm{N}}$, $I_f=Const$, $\cos\varphi=Const$ 时,$U=f(I)$ 的图像。
图像可以用相量图解释。
定义电压调整率 $ \Delta U=\frac{E_0-U_\mathrm{N}}{U_\mathrm{N}} $。
- 感性负载和纯电阻负载:外特性曲线下降
- 原因:电枢反应去磁,漏阻抗有压降
- 容性负载:外特性曲线可能上升
- 原因:电枢反应增磁
感性负载需要的励磁电流必定大于容性负载。
- 感性负载和纯电阻负载:外特性曲线下降
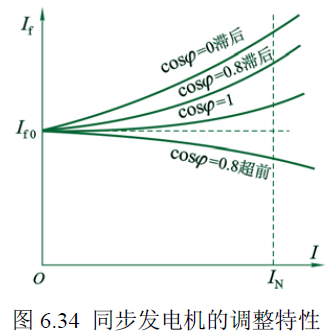
调整特性
图像为 $n=n_{\scriptscriptstyle\mathrm{N}}$, $U=Const$, $\cos\varphi=Const$ 时,$I_f=f(I)$ 的图像。
曲线上升下降趋势与外特性的相反。
参数计算
关于保梯电抗:知道它比漏电抗大就行了。
空载+短路特性求(直轴)同步电抗(不饱和)
短路时,$\dot{E}_0\approx\mathrm{j}\dot{I}_\mathrm{k}X_\mathrm{d} $,则有 $ X_\mathrm{d}=\displaystyle\frac{E_0}{I_\mathrm{k}} $。这里的 $E_0$ 是在气隙线上取得的。
空载+零功率因数特性求漏电抗
用特征三角形的直角边除以额定电流即可。
短路比
定义:产生额定空载电压与额定短路电流的两个励磁电流之比。
短路比一般在 0.5~1.5 之间,并且水轮机的短路比大于汽轮机。
短路比大,则同步电抗小,稳定程度高,气隙较大,转子额定励磁电流和用铜量就大;短路比小,则同步电抗大,稳定程度低,电压调整率大。
功角特性
在电枢反应一章,我们定义了功角 $\delta$,电磁功率可以用功角表示为
如果全部使用标幺值,则相数 $m$ 可以去掉。这一公式在电力系统暂态分析中会经常使用。公式的第一项称为基本电磁功率,第二项称为附加电磁功率。
关于稳定性,我们放到电力系统暂态分析中学习。
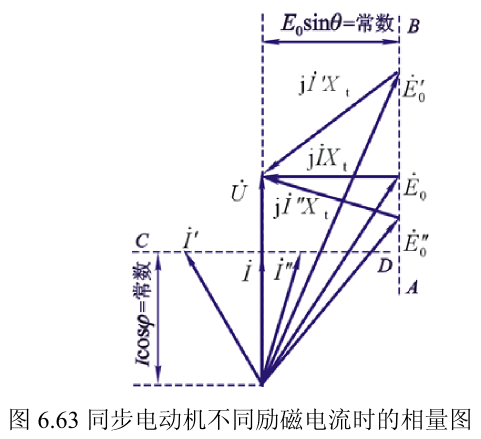
有功与无功的调节
有功只能通过调节原动机来调节,无功则是通过调节励磁电流来调节。
知道图中两个常数即可。
第六章 直流电机
直流电机的电枢绕组
为了改善电机的性能,我们希望用尽可能多的元件来组成电枢绕组,解决的办法是在电枢上采用多层绕组。为此引入“虚槽”的概念,如果一个槽内包含 $u$ 个元件边,则意味着一个实际的槽中含有 $u$ 个虚槽,即
电枢绕组的特点常用虚槽数、元件数、换向片数和各种节距来表示。一个换向片对应一个上元件边和下元件边,一个元件包含一个上元件边和下元件边,一个虚槽包含一个上元件边和个下元件边,因此三者数量相等,即
节距包括第一节距、第二节距、合成节距和换向节距。
第一节距 $y_1$
第一节距是指一个上元件边和下元件边在电枢圆周上所跨的距离,用虚槽数表示。为了使元件中的感应电动势最大,$y_1$ 所跨的距离应该接近一个极距,则有
一般我们会使用短距绕组。
第二节距 $y_2$
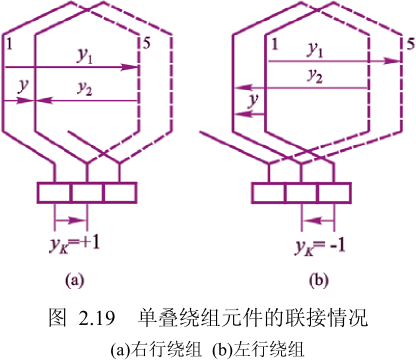
第二节距是指在同一个换向片上连接的下元件边到上元件边在电枢圆周上所跨的距离,用虚槽数表示。对于叠绕组,$y_2<0$;对于波绕组,$y_2>0$。
注:(b)图的 $y_1$ 指错了。合成节距 $y$
合成节距是指相串联的两个元件的对应边在电枢圆周上所跨的距离,用虚槽数表示,即 $y=y_1+y_2$ 。
换向节距 $y_\mathrm{k}$
换向节距是指在与每个元件相连的换向片在换向器上所跨的距离,用换向片数表示,换向节距与合成节距在数值上相等,即 $y_\mathrm{k}=y$ 。
单叠绕组是指 $y=y_\mathrm{k}=\pm 1$ 的叠绕组。
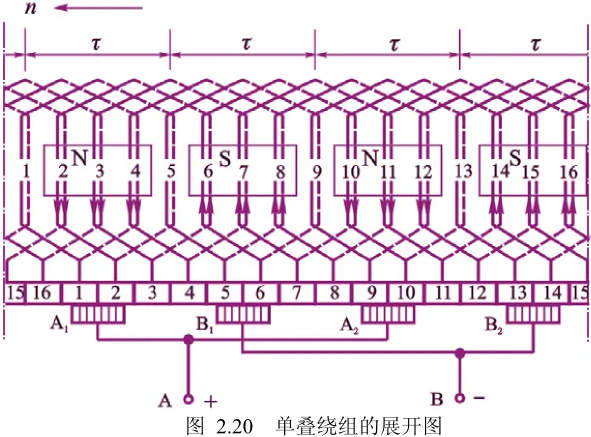
这里放一下绕组连接表和绕组展开图。
关于并联支路数,需要知道对于单叠绕组,并联支路数和极对数的关系为 $a=2p$ ;对于单波绕组,并联支路数为 $a=2$ 。
单波绕组不在学习大纲内。
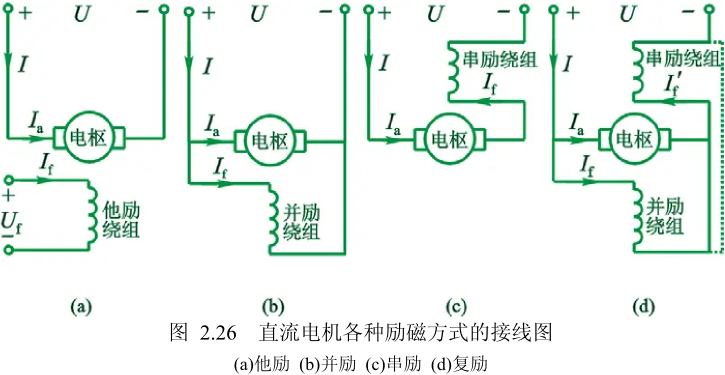
直流电机的励磁方式
直流电机的励磁方式有四种:他励、串励、并励和复励。
需要注意电枢电流、励磁电流和电源电流之间的关系。
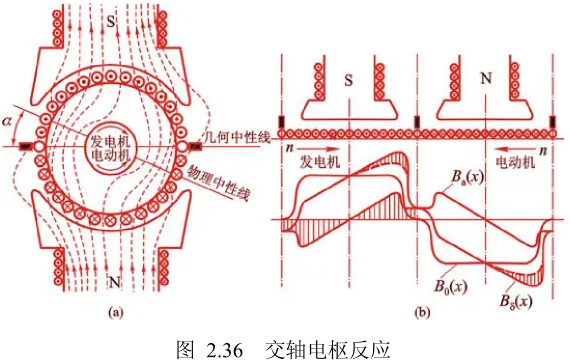
直流电机的电枢反应
这里直接放图,分析方法是沿着电刷切开铺平去分析。电枢反应同样包括直轴电枢反应和交轴电枢反应。
交轴电枢反应是去磁的,因为三角波增强磁场的那一部分会饱和,导致总磁通减少。
电动势和电磁转矩公式
直流电机的电动势公式为
其中 $N_\mathrm{a}$ 为电枢导体的总数,$a$ 为并联支路数。
电磁转矩公式为
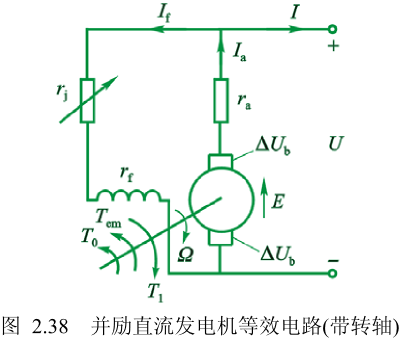
直流发电机基本方程
以并励直流发电机为例:
电枢回路的电动势平衡方程
励磁回路的电压方程
电流满足
剩下关于功率什么的都非常容易推导。