电气工程基础

第一章 基础知识

设备和线路的额定电压

设备额定电压：

如果线路的额定电压为 $U_\mathrm{N}$，则用电设备的额定电压也应该为 $U_\mathrm{N}$，线路首端的发电机的额定电压应为 $1.05U_\mathrm{N}$。

变压器额定电压：

	一次侧额定电压	二次侧额定电压
升压变压器	$1.05U_\mathrm{N}$	$1.1U_\mathrm{N}$
降压变压器	$U_\mathrm{N}$	$1.1U_\mathrm{N}$

变压器的二次侧相当于一台发电机，额定电压要比线路的额定电压略高，以抵抗线路的电压降。一般而言，变压器的二次侧额定电压为线路的1.1倍，小容量变压器可以是1.05倍。升压变压器一般会直连变压器，所以一次侧额定电压为1.05倍。

额定电压等级与平均额定电压等级

额定电压等级：3, 6, 10, 35, 110, 220, 330, 500.
平均额定电压等级：3.15, 6.3, 10.5, 37, 115, 230, 345, 525.

平均额定电压等级就是在额定电压等级的基础上乘了个1.05，然后取最相近的整数。

交流电的瞬时功率

$$\begin{align*} p&=ui=u_mi_m\sin{\omega t}\sin(\omega t-\varphi) \\ &=\frac{1}{2}u_mi_m\left[\cos\varphi-\cos(2\omega t-\varphi)\right]\\ &=UI\cos\varphi - UI\cos(2\omega t-\varphi) \\ &=UI\cos\varphi - UI\left[\cos{2\omega t}\cos\varphi-\sin{2\omega t}\sin\varphi\right] \\ &=UI\cos\varphi(1-\cos{2\omega t}) - UI\sin\varphi\sin{2\omega t} \\ &=p_{_P}-p_{_Q} \end{align*}$$

交流传输

假如一段线路上没有有功损耗，那么我们可以用以下公式计算传递的功率。

$$P=\frac{U_1U_2}{X_L}\sin\delta$$

交流电输送的条件：线路的始端与末端电压之间必须存在相位角。

标幺制

在电力系统分析中，基值一般选取容量和电压。

	相参数	线参数
基准容量	$S_\mathrm{\varphi b}=U_\mathrm{\varphi b}I_\mathrm{\varphi b}$	$S_\mathrm{b}=\sqrt{3}U_\mathrm{b}I_\mathrm{b}$
基准电压	$U_\mathrm{\varphi b}=I_\mathrm{\varphi b}Z_\mathrm{\varphi b}$	$U_\mathrm{b}=\sqrt{3}I_\mathrm{b}Z_\mathrm{b}$

在设置好基值后，计算中就不需要加入任何系数了。

在不同电压等级的线路中，基准值不同，计算时需要统一归算到同一个基准值下。如果使用额定电压等级，归算方法为“标幺值->实际值->标幺值”；如果使用平均额定电压等级，则直接用容量归算，即 $x=x’\frac{S}{S’}$

年持续负荷曲线

可以用于计算年最大负荷利用小时数。

$$T_\mathrm{max}=\frac{A}{P_\mathrm{max}}=\frac{\int_{0}^{8760}{P(t)}\mathrm{d}t}{P_\mathrm{max}}$$

用于估算全网年用电量。

第二章 三相电路的参数计算

三相输电线路

电阻

$$r=\frac{\rho l}{S}$$

如果温度不是 20℃，则需要进行温度修正。

$$r_t=r_{20}\left[1+\alpha(t-20)\right]$$

其中，$\alpha$ 为电阻温度系数。

电抗

在计算电抗时，我们需要用到自几何均距

$$r'=r\mathrm{e}^{-\frac{1}{4}}$$

其中，$r$ 为导线的半径。

导线的几何均距

$$D_\mathrm{eq}=\sqrt[3]{D_{12}D_{23}D_{13}}$$

其中，$D_{12}$, $D_{23}$, $D_{13}$ 分别为三相导线等效中心之间的距离。

导线的等效半径

$$R_s=\sqrt[n]{r'\cdot n\cdot d^{n-1}}$$

其中，$d$ 为分裂导线之间的距离，$n$ 为分裂导线分裂的根数。

导线单位长度电抗的计算公式

$$x=0.1445\lg\frac{D_\mathrm{eq}}{R_s}\quad(\Omega/\mathrm{km})$$

电纳

导线单位长度电纳的计算公式

$$b=\frac{7.58\times10^{-6}}{\lg\displaystyle\frac{D_\mathrm{eq}}{R_s}}$$

其中，$D_\mathrm{eq}$ 与电抗计算中的值一致，而 $R_s=\sqrt[n]{r\cdot n\cdot d^{n-1}}$，不需要再使用自几何均距了。

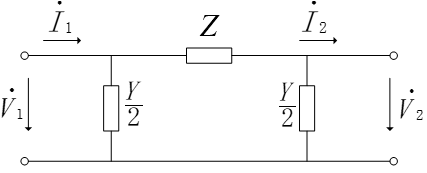
$\Pi$ 模型

记单位长度阻抗 $z=r+\mathrm{j}x$，单位长度导纳 $y=g+\mathrm{j}b$，则有传输常数$ \gamma=\sqrt{zy}=\alpha+\mathrm{j}\beta $。其中，$\alpha$ 为衰减系数，$\beta$ 为相移系数。（这一部分了解即可）

记波阻抗 $Z_c=\sqrt{\frac{z}{y}}$，则有 $\Pi$ 形输电线路模型参数

$$Z=Z_c\sinh{\gamma l}$$ $$Y=\frac{2(\cosh{\gamma l}-1)}{Z_c\sinh{\gamma l}}$$

三相变压器

变压器的铭牌会告诉我们额定容量 $S_\mathrm{N}$、额定电压 $U_\mathrm{N}$、额定电流 $I_\mathrm{N}$、额定频率 $f_\mathrm{N}$ 等参数，这些是已知的。

电阻

通过短路试验得到短路功率 $P_\mathrm{k}$，此时电流为额定电流，那么短路功率可以表示为

$$P_\mathrm{k}=3I_\mathrm{N}^2R_\mathrm{T}=\frac{S_\mathrm{N}^2}{U_\mathrm{N}^2}R_\mathrm{T}$$

如果短路功率单位为 kW，额定容量单位为 MVA，额定电压单位为 kV，则有

$$R_\mathrm{T}=\frac{P_\mathrm{k}}{1000}\frac{U_\mathrm{N}^2}{S_\mathrm{N}^2}$$

用标幺值表示为

$$R_\mathrm{T}=\frac{P_\mathrm{k}}{1000S_\mathrm{N}}$$

电抗

通过短路试验得到短路电压百分比 $U_\mathrm{k}\%$，短路电压百分比可以表示为

$$U_\mathrm{k}\%=\frac{\sqrt{3}I_\mathrm{N}Z_\mathrm{T}}{U_\mathrm{N}}\times 100 \approx \frac{\sqrt{3}I_\mathrm{N}X_\mathrm{T}}{U_\mathrm{N}}\times 100$$

其中，能使用约等于的原因是变压器的电阻一般很小，电压降落基本都在电抗上。由此可以计算出电抗

$$X_\mathrm{T}=\frac{U_\mathrm{k}\%}{100}\cdot\frac{U_\mathrm{N}}{\sqrt{3}I_\mathrm{N}}=\frac{U_\mathrm{k}\%}{100}\cdot\frac{U_\mathrm{N}^2}{S_\mathrm{N}}$$

用标幺值表示为

$$X_\mathrm{T}=\frac{U_\mathrm{k}\%}{100}$$

电导

通过空载试验得到空载功率 $P_\mathrm{0}$，此时电压为额定电压，那么空载功率可以表示为

$$P_\mathrm{0}=U_\mathrm{N}^2G_\mathrm{T}$$

如果空载功率单位为 kW，额定电压单位为 kV，则有

$$G_\mathrm{T}=\frac{P_\mathrm{0}}{1000U_\mathrm{N}^2}$$

用标幺值表示为

$$G_\mathrm{T}=\frac{P_\mathrm{0}}{1000S_\mathrm{N}}$$

电纳

通过空载试验得到空载电流百分比 $I_\mathrm{0}\%$，空载电流百分比可以表示为

$$I_\mathrm{0}\%=\frac{U_\mathrm{N}Y_\mathrm{T}}{\sqrt{3}I_\mathrm{N}}\times 100 \approx \frac{U_\mathrm{N}B_\mathrm{T}}{\sqrt{3}I_\mathrm{N}}\times 100$$

其中，能使用约等于的原因是变压器的电导一般很小，电流基本流过电纳。由此可以计算出电纳

$$B_\mathrm{T}=\frac{I_\mathrm{0}\%}{100}\cdot\frac{\sqrt{3}I_\mathrm{N}}{U_\mathrm{N}}=\frac{I_\mathrm{0}\%}{100}\cdot\frac{S_\mathrm{N}}{U_\mathrm{N}^2}$$

用标幺值表示为

$$B_\mathrm{T}=\frac{I_\mathrm{0}\%}{100}$$

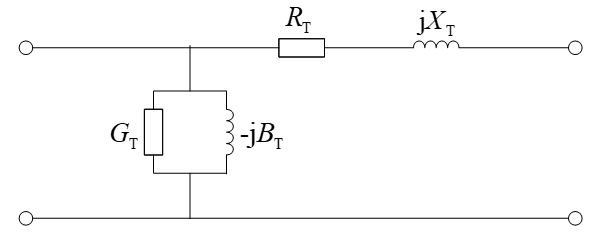
现在我们就可以得到三相变压器模型了。

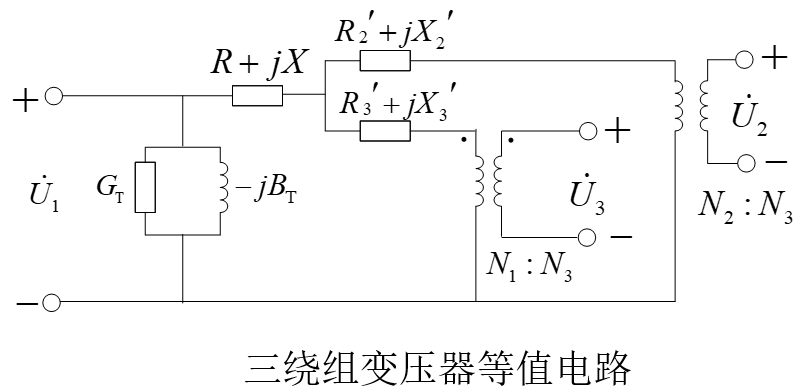
三相三绕组变压器模型

三绕组变压器可以连接三个电压等级的电网。三个绕组的容量不一定相等，中压和低压绕组有可能是高压容量的 50%，因此需要容量归算。同时，空载实验和短路实验在两个绕组间进行，另一个绕组开路，因此会算出三组数据。

电阻

首先，我们假设三个绕组的容量相等。

由于是三绕组，会有三个短路功率。

$$\begin{cases} P_\mathrm{k(1-2)}=P_\mathrm{k1}+P_\mathrm{k2} \\ \\ P_\mathrm{k(1-3)}=P_\mathrm{k1}+P_\mathrm{k3} \\ \\ P_\mathrm{k(2-3)}=P_\mathrm{k2}+P_\mathrm{k3} \end{cases}$$

可以计算出每个绕组分别的短路功率，然后就可以使用双绕组变压器的计算方式计算电阻了。

如果三个绕组容量不相等，需要进行容量归算。我们以一个100/50/100类型变压器为例，其中压绕组容量只有 50%，则有

$$\begin{cases} P_\mathrm{k(1-2)}=P_\mathrm{k(1-2)}'\left(\displaystyle\frac{S_\mathrm{N}}{0.5S_\mathrm{N}}\right)^2=4P_\mathrm{k(1-2)}' \\ \\ P_\mathrm{k(2-3)}=P_\mathrm{k(2-3)}'\left(\displaystyle\frac{S_\mathrm{N}}{0.5S_\mathrm{N}}\right)^2=4P_\mathrm{k(2-3)}' \end{cases}$$

电抗

国标要求，铭牌上提供的短路电压百分数已经是归算后的数值，因此不必进行容量归算。

与短路功率类似，短路电压百分数也有三个

$$\begin{cases} U_\mathrm{k(1-2)}\%=U_\mathrm{k1}\%+U_\mathrm{k2}\% \\ \\ U_\mathrm{k(1-3)}\%=U_\mathrm{k1}\%+U_\mathrm{k3}\% \\ \\ U_\mathrm{k(2-3)}\%=U_\mathrm{k2}\%+U_\mathrm{k3}\% \end{cases}$$

自耦变压器的参数计算与普通变压器没有什么不同。

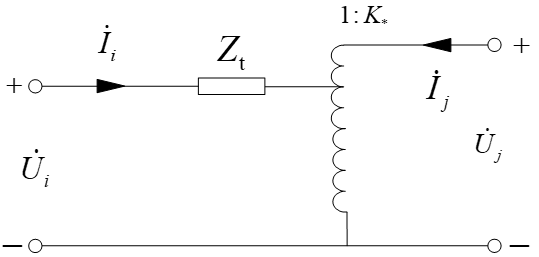
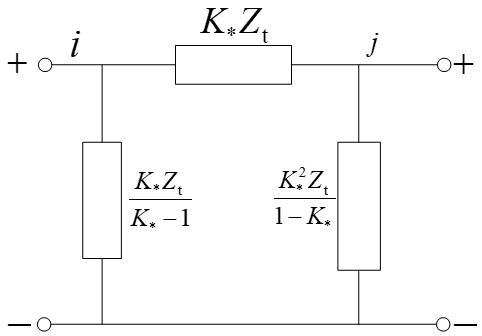
变压器非标准变比的 $\Pi$ 模型

左右两个阻抗加起来为 $-K_*Z_\mathrm{T}$。

第三章 电力系统接线

在电力系统接线中，隔离开关（刀闸）和断路器是两个重要的设备。断路器可以在带有负载的情况下切断线路；而隔离开关只能在没有负载的情况下切断线路，因为其不具有灭弧能力，其作用是形成一个明显的隔离点。

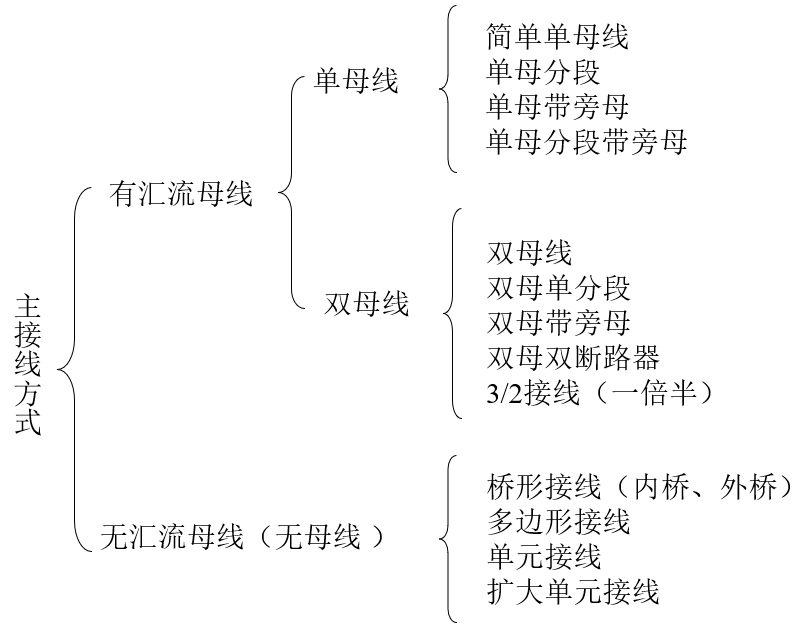
电力系统的接线包含以下类型：

我们选取几个典型的接线方式图片。

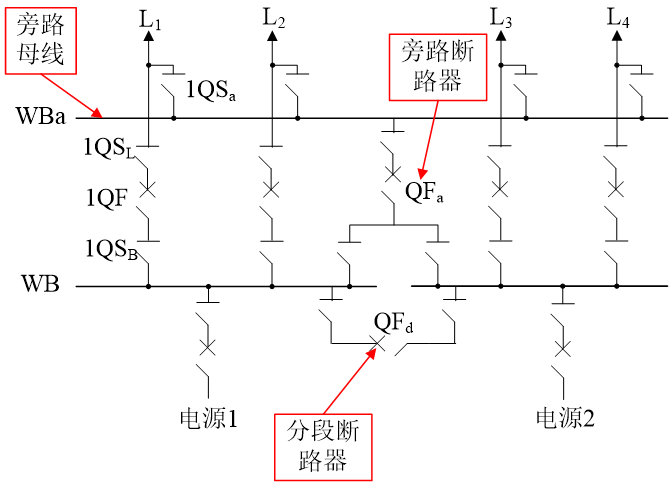
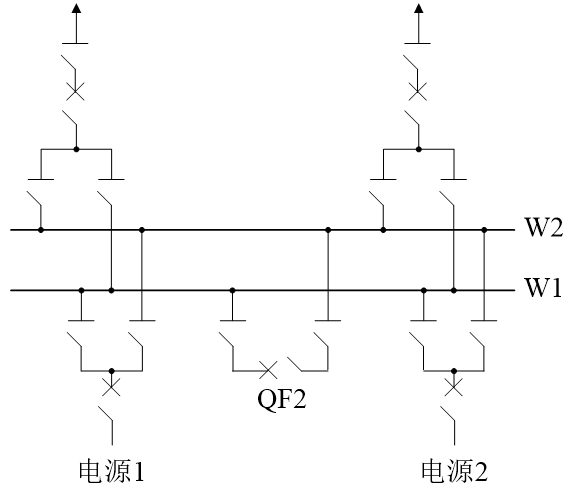
单母线分段带旁路母线

实际上，现在带旁路母线的接线方式已经不多见了，但还是要了解一下。

双母线接线

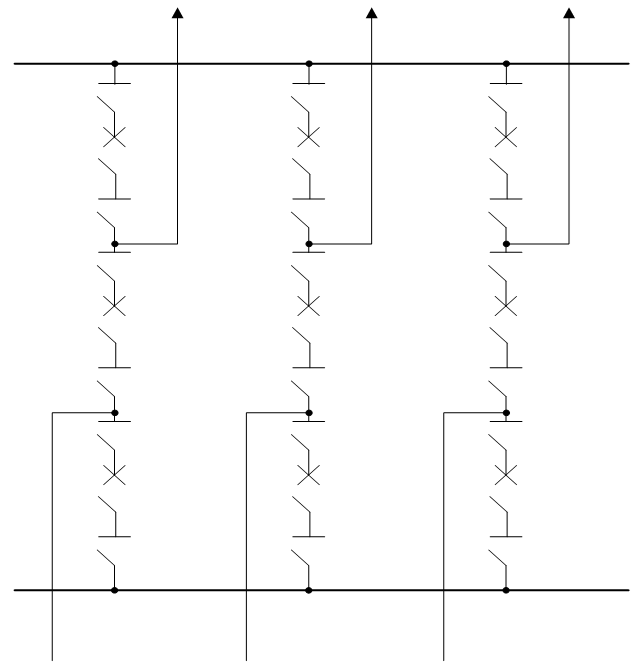
3/2 接线

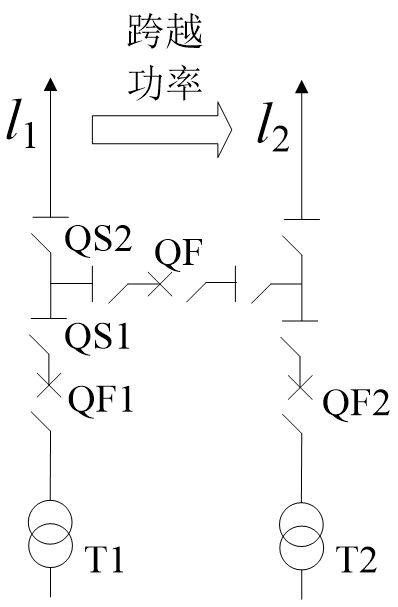
外桥接线

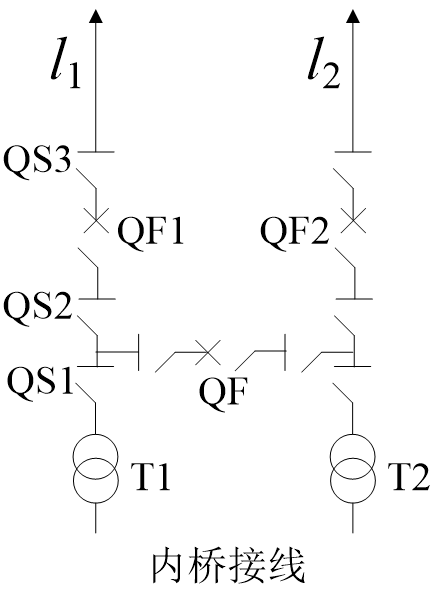
内桥接线

第四章 潮流计算

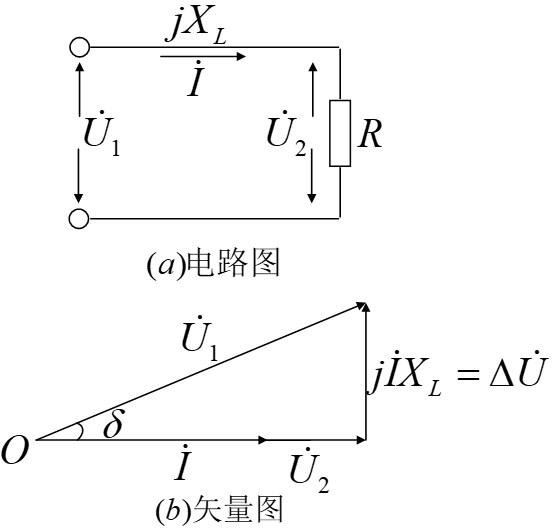
电压降落

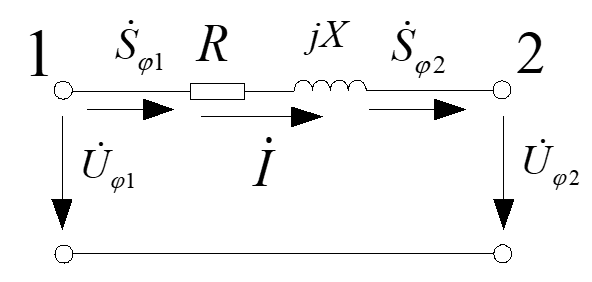
一切的根本，就是以下两个公式

$$\Delta\dot{U}=\dot{U}_1-\dot{U}_2=\dot{I}(R+\mathrm{j}X)$$ $$\dot{I}=\left(\frac{\dot{S}_1}{\dot{U}_1}\right)^*=\left(\frac{\dot{S}_2}{\dot{U}_2}\right)^*$$

在潮流计算中，我们默认下标“1”的为送端（始端），下标“2”的为受端（末端）。

已知受端电压和功率

定义纵分量

$$\Delta U=\frac{P_2R+Q_2X}{U_2}$$

横分量

$$\delta U=\frac{P_2X-Q_2R}{U_2}$$

纵分量为压降的实部，纵向定义为功率传输的方向；横分量为压降的虚部，横向定义为功率传输垂直的方向。

那么，在已知受端电压和功率的情况下，送端电压可以表示为

$$\dot{U}_1=\dot{U}_2+\Delta U+\mathrm{j}\delta U$$

在 110 kV 及以下电压等级中，横分量可以直接省略。

已知送端电压和功率

定义纵分量

$$\Delta U=\frac{P_1R+Q_1X}{U_1}$$

横分量

$$\delta U=\frac{P_1X-Q_1R}{U_1}$$

那么，在已知送端电压和功率的情况下，受端电压可以表示为

$$\dot{U}_2=\dot{U}_1-(\Delta U+\mathrm{j}\delta U)$$

已知送端电压和受端功率

这时候需要使用迭代法计算，一般而言迭代一次足矣。迭代步骤如下：

1. 假设各节点电压均为额定电压
2. 从后往前计算功率分布
3. 计算完功率流后，再从前往后计算电压降落

电压指标

$$\text{电压损耗率%}=\displaystyle\frac{U_1-U_2}{U_\mathrm{N}}\times 100$$ $$\text{始端电压偏移%}=\displaystyle\frac{U_1-U_\mathrm{N}}{U_\mathrm{N}}\times 100$$ $$\text{末端电压偏移%}=\displaystyle\frac{U_2-U_\mathrm{N}}{U_\mathrm{N}}\times 100$$ $$\text{电压调整%}=\displaystyle\frac{U_{20}-U_2}{U_N}\times 100$$

功率损耗

功率损耗可以通过以下公式计算

$$\Delta\dot{S}=\frac{P^2+Q^2}{U^2}(R+\mathrm{j}X)$$

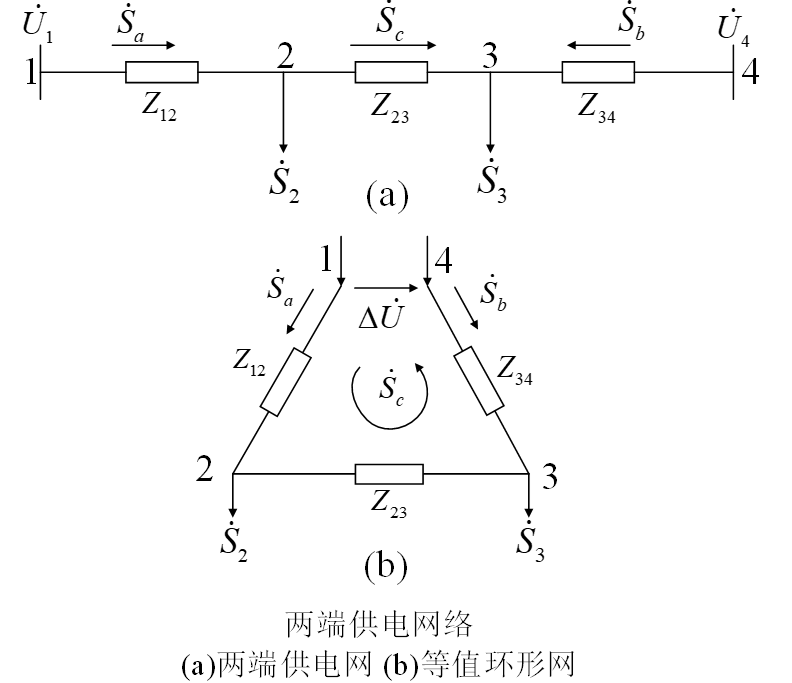
闭式电网与两端供电电网

方法：列KVL，计算电网功率分界点，然后分成两个开式电网进行迭代。

首先，假设全网的电压均为 $U_\mathrm{N}$，对环形网列KVL

$$\dot{I}_aZ_{12}+(\dot{I}_a-\dot{I}_2)Z_{23}+(\dot{I}_a-\dot{I}_2-\dot{I}_3)Z_{34}=\Delta\dot{U}$$

两端取共轭，同时乘以 $U_\mathrm{N}$，有

$$\dot{S}_aZ_{12}^*+(\dot{S}_a-\dot{S}_2)Z_{23}^*+(\dot{S}_a-\dot{S}_2-\dot{S}_3)Z_{34}^*=U_\mathrm{N}\Delta\dot{U}^*$$

得到

$$\dot{S}_a=\frac{(Z_{23}^*+Z_{34}^*)\dot{S}_2+Z_{34}^*\dot{S}_3}{Z_{12}^*+Z_{23}^*+Z_{34}^*}+\frac{U_\mathrm{N}\Delta\dot{U}^*}{Z_{12}^*+Z_{23}^*+Z_{34}^*}$$

式子的第二项为循环功率，$\Delta\dot{U}=\dot{U}_1-\dot{U}_4$。

计算完成后，从无功分界点可以开环，再按照开式网迭代法进行计算。

导纳矩阵

使用计算机求解潮流分布时，通常会使用导纳矩阵来表示电网的拓扑结构。导纳矩阵的元素 $y_{ij}$ 表示节点 $i$ 和节点 $j$ 之间的导纳。如果 $i=j$，则 $y_{ii}$ 为节点 $i$ 的自导纳，是一个正值；如果 $i\neq j$，则 $y_{ij}$ 为节点 $i$ 和节点 $j$ 之间的互导纳，是一个负值。

导纳矩阵是一个对称矩阵。

导纳矩阵的修改，只需要关注串联一个变压器这个操作。这与变压器非标准变比一节的计算方法一致。计算的时候不要忘了阻抗的虚部要加 $\mathrm{j}$。

第五章 火电机组有功调整

知道几个概念和等耗量微增率原则即可。

耗量特性：“原料”投入 $F$ 与功率产出 $P$ 之间的关系。

比耗量：$\mu=\frac{F}{P}$，表示每单位功率的原料投入量。

机组效率：$\eta=\frac{P}{F}$，表示每单位原料投入的功率产出。

耗量微增率：$\lambda=\frac{\mathrm{d} F}{\mathrm{d} P}$

等耗量微增率原则

目标函数

$$\min \sum_{i=1}^{n} F_i(P_i)$$

使得

$$\begin{cases} \Sigma P_i-P_\mathrm{L}-\Delta P_\mathrm{L}=0 \\ \\ P_{i,\min}\leq P_i\leq P_{i,\max} \end{cases}$$

求解，得到

$$\lambda=\frac{\mathrm{d} F_i(P_i)}{\mathrm{d} P_i}(1-\frac{\partial \Delta P_\mathrm{L}}{\partial P_i})^{-1}$$

其中，$P_\mathrm{L}$ 为目标负载，$\Delta P_\mathrm{L}$ 为网络损耗。

第六章 无功补偿与调压

系统的电压与无功功率息息相关。前面我们也学习过，线路上的压降主要是传输无功功率导致的，因此我们希望线路上尽可能少的传输无功，而在用电侧就地补偿无功功率。

电压调节方式

在电网的中枢点，我们有以下三种调压方式：

1. 逆调压

   高负荷时升高中枢点电压，大约比额定电压高 5%；低负荷时降低中枢点电压，一般为额定电压。记作 (5%, 0)。

2. 顺调压

   高负荷时降低中枢点电压，大约比额定电压高 2.5%；低负荷时升高中枢点电压，大约比额定电压高 7.5%。记作 (2.5%, 7.5%)。

3. 恒调压

   中枢点电压基本不变，大约比额定电压高 2%~5% 。

调节变压器分接头调压

修改变压器分接头实际上是在调整电网的无功分布，因此需要电网有充足的无功功率。否则盲目调高变比，会导致电网其他位置电压下降，造成严重事故。

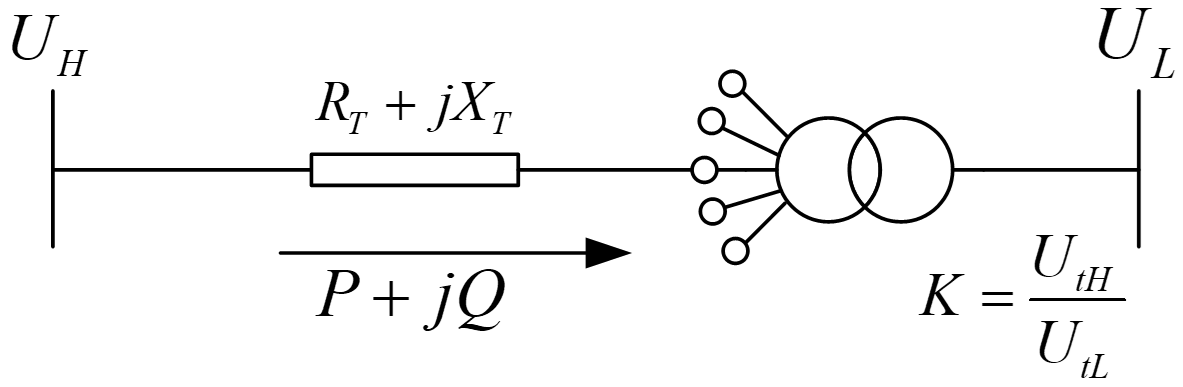
降压变压器

如图，高压侧电压为 $U_\mathrm{H}$，大小由电网决定；低压侧希望电压为 $U_\mathrm{L}$。$U_\mathrm{tH}$ 和 $U_\mathrm{tL}$ 为变压器的分接头电压，变比为 $K=\displaystyle\frac{U_\mathrm{tH}}{U_\mathrm{tL}}$。一般而言，$U_\mathrm{tL}$ 只有一个档位可选，而 $U_\mathrm{tH}$ 有多个档位可选。

计算纵分量

$$\Delta U=\frac{P_\mathrm{}R+Q_\mathrm{}X}{U_\mathrm{H}}$$

横分量直接忽略，则对于变压器有

$$\frac{U_\mathrm{H}-\Delta U}{U_\mathrm{L}}=\frac{U_\mathrm{tH}}{U_\mathrm{tL}}$$

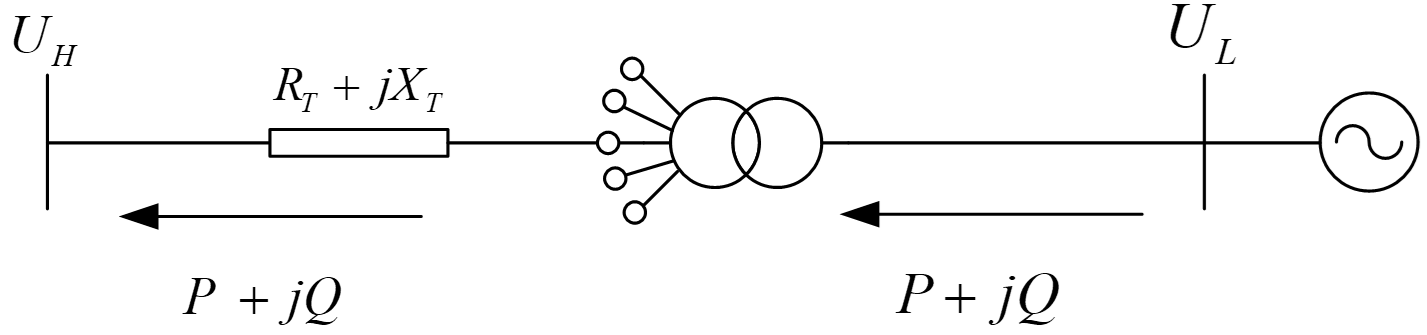
升压变压器

与降压变压器类似，先计算纵分量

$$\Delta U=\frac{PR+QX}{U_\mathrm{H}}$$

横分量直接忽略，则对于变压器有

$$\frac{U_\mathrm{H}+\Delta U}{U_\mathrm{L}}=\frac{U_\mathrm{tH}}{U_\mathrm{tL}}$$

对于有载调压，我们需要在高负荷和低负荷时，分别算出二者对应的分接头；而无载调压则只需要算出一个分接头，即高负荷和低负荷时的平均接头。

调相机调压

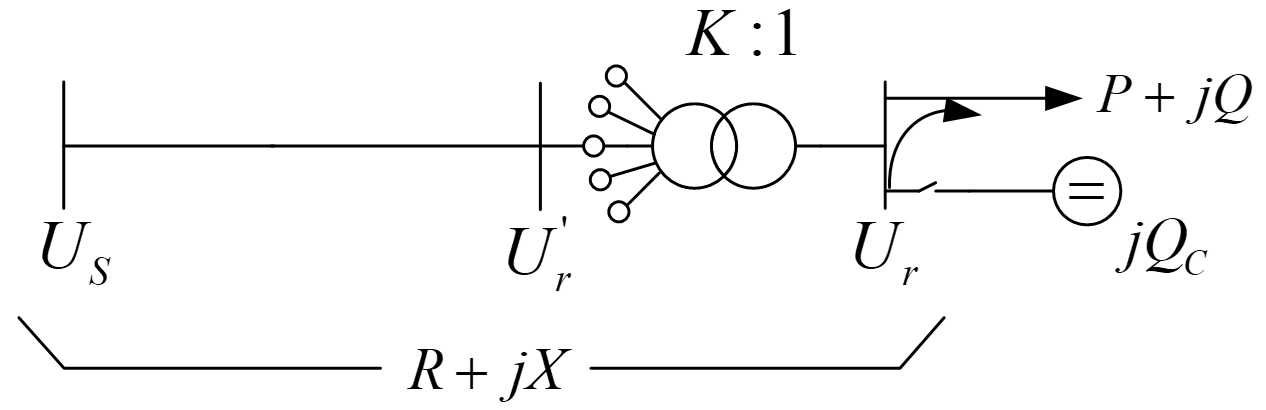
如图，$U_\mathrm{s}$ 为高压侧电压；$U_\mathrm{r}$ 为低压侧电压，归算到高压侧时为 $U_\mathrm{r}’$ ；负荷侧用电需求为 $P+\mathrm{j}Q$。

补偿前：

$$U_\mathrm{s}=U_\mathrm{r}'+\frac{PR+QX}{U_\mathrm{r}'}$$

补偿后：

$$U_\mathrm{s}=U_\mathrm{rc}'+\frac{PR+(Q-Q_\mathrm{c})X}{U_\mathrm{rc}'}$$

其中，$U_\mathrm{rc}’$ 为低压侧希望电压。

联立方程，解得

$$Q_\mathrm{c}=\frac{U_\mathrm{rc}}{X}\left(U_\mathrm{rc}-\frac{U_\mathrm{r}'}{K}\right)K^2$$

一般我们会把调相机欠励容量设为过励容量的一半，即

$$\begin{cases} \displaystyle{ Q_\mathrm{c}=\frac{U_\mathrm{rc,M}}{X}\left(U_\mathrm{rc,M}-\frac{U_\mathrm{rM}'}{K}\right)K^2} \\ \\ \displaystyle{ -\frac{1}{2}Q_\mathrm{c}=\frac{U_\mathrm{rc,m}}{X}\left(U_\mathrm{rc,m}-\frac{U_\mathrm{rm}'}{K}\right)K^2 } \end{cases}$$

联立有

$$\frac{U_\mathrm{rc,M}(KU_\mathrm{rc,M}-U_\mathrm{rM}')}{U_\mathrm{rc,m}(KU_\mathrm{rc,m}-U_\mathrm{rm}')}=-2$$

由此确定 K 值，再计算 $Q_\mathrm{c}$。

投切电容器调压

原理图与调相机调压一样。

原则：最小负荷全切除，最大负荷定容量。

在最小负荷时，切除全部电容器，此时确定变压器变比以满足最小负荷时的调压需求；在最大负荷时，投入电容器，此时变压器变比不再改变，确定电容器容量。

最小负荷：

$$K=\frac{U_\mathrm{tH}}{U_\mathrm{tL}}=\frac{U_\mathrm{rm}'}{U_\mathrm{rc,m}}$$

最大负荷：

$$Q_\mathrm{c}=\frac{U_\mathrm{rc,M}}{X}\left(U_\mathrm{rc,M}-\frac{U_\mathrm{rM}'}{K}\right)K^2$$

第七章 不对称短路

不对称短路是指在三相电力系统中，发生了某一相或两相的短路。常见的不对称短路有单相接地短路、两相短路和两相接地短路。

对称分量法

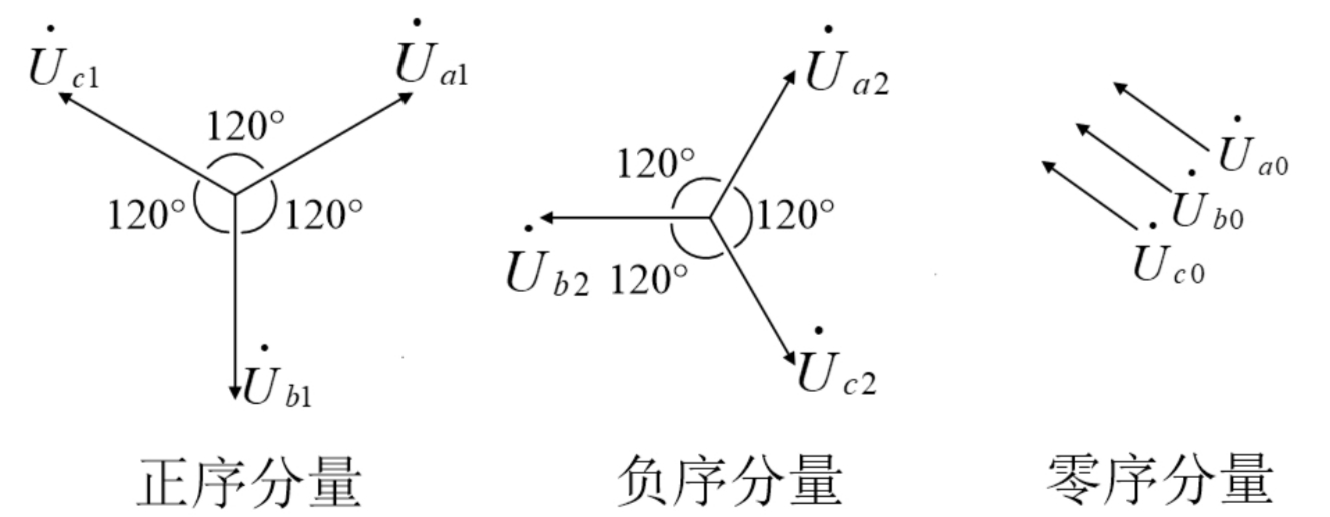
对称分量法是分析不对称短路的一种方法。它将三相电流和电压分解为正序、负序和零序分量。

正序分量顺时针、逆序分量逆时针。

记 $\alpha=\mathrm{e}^{\mathrm{j}120^\circ}$，则有

$$\begin{bmatrix} \dot{U}_a \\ \dot{U}_b \\ \dot{U}_c \end{bmatrix}= \begin{bmatrix} 1 & 1 & 1\\ 1 & \alpha^2 & \alpha \\ 1 & \alpha & \alpha^2 \end{bmatrix} \begin{bmatrix} \dot{U}_{a0} \\ \dot{U}_{a1} \\ \dot{U}_{a2} \end{bmatrix}$$

即

$$\mathbf{U}_{abc}=\mathbf{TU}_{012}$$

矩阵 $\mathbf{T}$ 为对称分量变换矩阵，其逆矩阵为

$$\mathbf{T}^{-1}=\frac{1}{3} \begin{bmatrix} 1 & 1 & 1\\ 1 & \alpha & \alpha^2 \\ 1 & \alpha^2 & \alpha \end{bmatrix}$$

序网的建立

这一部分以看书为主，需要会画序网图。

电动势和各序电压满足：

$$\begin{bmatrix} \dot{U}_{a0} \\ \dot{U}_{a1} \\ \dot{U}_{a2} \end{bmatrix}= \begin{bmatrix} 0 \\ \dot{E}_{1\Sigma} \\ 0 \end{bmatrix}- \begin{bmatrix} Z_{0\Sigma}\dot{I}_{a0} \\ Z_{1\Sigma}\dot{I}_{a1} \\ Z_{2\Sigma}\dot{I}_{a2} \end{bmatrix}$$

不对称故障

为了便于计算，我们需要寻找一个特殊相。如果是单相故障，则特殊相为故障相；如果是两相故障，则特殊相为非故障相。这里我们都以 A 相为特殊相。

单相接地短路

边界条件：

$$\begin{cases} \dot{U}_{a}=Z_\mathrm{k}\dot{I}_{a}=0 \\ \\ \dot{I}_{b}=\dot{I}_{c}=0 \end{cases}$$

根据对称分量法，单相接地短路相当于三序网串联，序网图为

两相短路

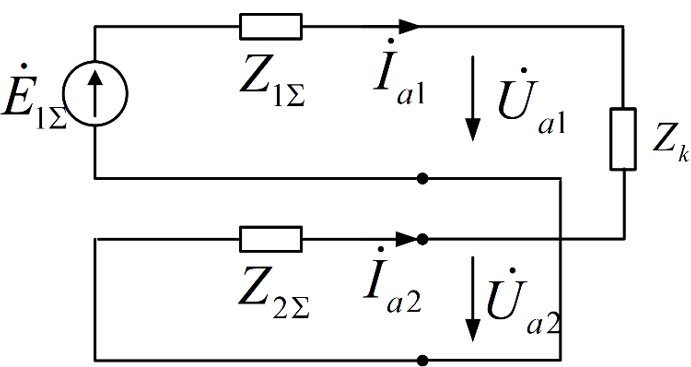
边界条件：

$$\begin{cases} \dot{I}_{a}=0\\ \\ \dot{I}_{b}+\dot{I}_{c}=0 \\ \\ \dot{U}_{b}-\dot{I}_bZ_\mathrm{k} =\dot{U}_{c} \end{cases}$$

根据对称分量法，两相短路相当于正序网与负序网串联，序网图为

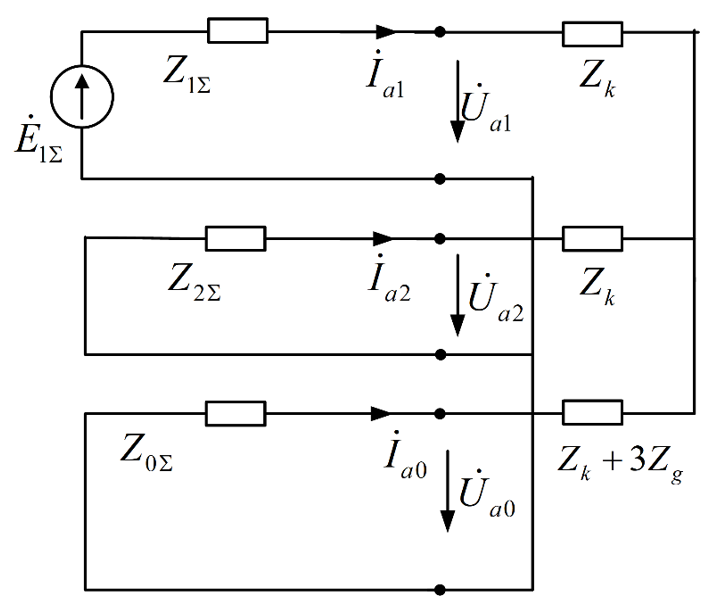
两相接地短路

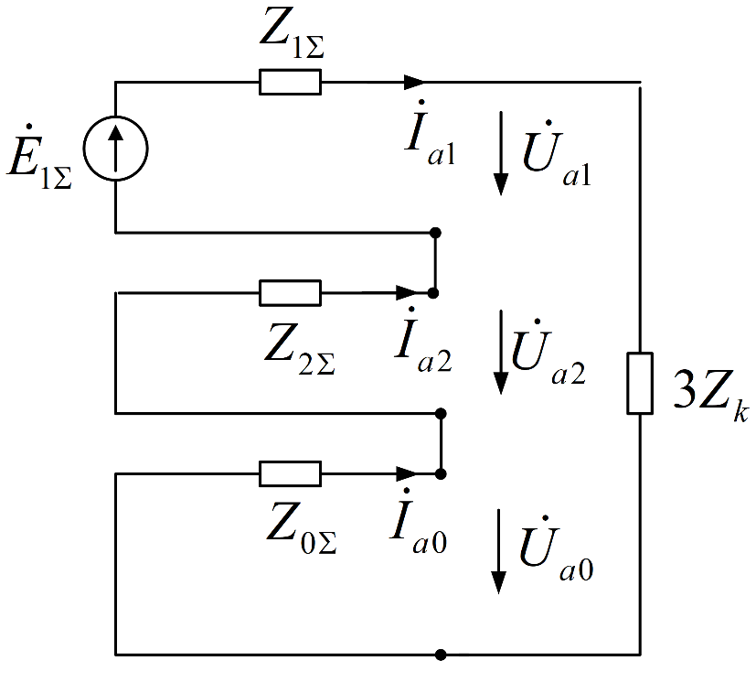
边界条件：

$$\begin{cases} \dot{I}_{a}=0\\ \\ \dot{U}_{b}=Z_\mathrm{k}\dot{I}_b + Z_\mathrm{g}(\dot{I}_b+\dot{I}_c) \\ \\ \dot{U}_{c}=Z_\mathrm{k}\dot{I}_c + Z_\mathrm{g}(\dot{I}_b+\dot{I}_c) \end{cases}$$

根据对称分量法，两相接地短路相当于三序网并联，序网图为

正序等效定则

以上三种故障的正序电流均可表示为 $\dot{I}_{a1}=\displaystyle\frac{\dot{E}_{1\Sigma}}{Z_{1\Sigma}+Z_\Delta}$，其中 $\dot{E}_{1\Sigma}$ 为正序电动势。

故障相电流的绝对值 $I_\mathrm{k}$ 可以表示为 $I_\mathrm{k}=mI_{a1}$ 。

故障类型	$Z_\Delta$	$m$
三相短路	0	1
单相接地短路	$Z_{2\Sigma}+Z_{0\Sigma}+3Z_\mathrm{k}$	3
两相短路	$Z_{2\Sigma}+Z_\mathrm{k}$	$\sqrt{3}$
两相接地短路	$Z_\mathrm{k}+(Z_{2\Sigma}+Z_\mathrm{k})\parallel(Z_{0\Sigma}+Z_\mathrm{k}+3Z_\mathrm{g})$	$\sqrt{3}\sqrt{1-\displaystyle\frac{Z_{2\Sigma}Z_{0\Sigma}}{(Z_{2\Sigma}+Z_{0\Sigma})^2}}$

电压流过变压器后的相位变化

铭记忘记相位扣了20分的教训！

1. Y/Y-12

   正负零序电压相位均不变。

2. Y/$\Delta$-11:

   从 Y 侧到 $\Delta$ 侧，正序电压逆时针转 30°，负序电压顺时针转 30°，零序电压不变。