高电压技术
均匀电场中的放电
电介质
电介质常用作绝缘材料。
电介质的分类:
- 按物质形态分
- 固体
- 液体
- 气体
气体在击穿后有完全的绝缘自恢复特性。
- 按在电气设备中所处的位置分
- 外绝缘:一般由气体(空气、SF6等)和固体(绝缘子、绝缘套管等)联合构成
- 内绝缘:一般由液体(油、变压器油等)和固体(绝缘纸、绝缘板等)联合构成
电介质在电场作用下出现的现象:
- 弱电场:极化、电导、介质损耗
- 强电场:放电、闪络、击穿
击穿:同一绝缘介质内部发生的贯穿性放电。
闪络:沿两种绝缘介质界面发生的自持放电(沿面放电发展到贯穿性的空气击穿)。
气体介质在纯净、中性状态下不导电。
带电粒子
带电粒子的产生
原子的激励与电离
- 激励:原子吸收能量后,电子跃迁到更高的能级,但仍在原子核的束缚范围内。 $W_\mathrm{e}$ 为激励能。
- 电离:原子吸收足够的能量后,电子完全脱离原子核的束缚,形成自由电子和正离子。 $W_\mathrm{i}$ 为电离能。
气体电离的四种形式
- 光电离:光子能量大于或等于气体分子电离能时,光子与气体分子相互作用,导致电子脱离,即 $h\nu > W_\mathrm{i}$ 。
- 热电离:气体分子在高温下获得足够的动能,克服束缚能量,电子脱离原子核。温度一般满足 $T > 10^4\ \mathrm{K}$。
- 电子碰撞电离:气体中产生带电粒子最重要的方式,主要由电子完成。自由电子与气体分子碰撞,能量足够时使分子电离。提高外加电压会使碰撞电离的概率增大。
- 电极表面电离:正离子撞击阴极表面,使表面原子电离,释放出电子。主要包括光电效应、阴极射线、热电子发射和强场发射。
带电粒子在气体中的运动
自由行程长度
自由行程长度:两次碰撞间走过的距离。
平均自由行程长度:单位行程中,碰撞次数的倒数 $\lambda$ 。
实际的自由行程长度是一个随机量,有很大的分散性。粒子的自由行程长度大于等于某一距离 $x$ 的概率为
由气体动力学可知,电子的平均自由行程长度为
其中,$r$ 为气体分子半径,$N$ 为气体分子密度。
带电粒子的迁移率
迁移率 $k$ 表示带电粒子在单位场强的作用下沿电场方向的漂移速度。
带电粒子的扩散
压强越小,温度越高,气体扩散越快。
电子热运动速度快,自由行程长度大,扩散远快于离子。
带电粒子的消失
主要包括:在电极上形成电流、扩散逸出气体放电空间、复合和附着形成负离子。
放电
汤逊气体放电理论
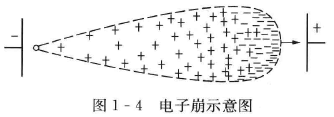
电子崩 ($\alpha$ 过程)
电子崩是指在电场作用下,电子与气体分子碰撞,产生新的自由电子和正离子。这个过程是放电的起始阶段,属于空间电离。
在高气压和高真空下,气体具有较高的电气强度。
电子崩从阴极开始,电子向阳极运动、正离子向阴极运动。因此崩头为电子,崩尾为正离子。
电子碰撞电离系数 $\alpha$ :一个电子沿电场方向运动 1 cm 的行程中所完成的碰撞次数平均值。
自持放电 ($\gamma$ 过程)
自持放电属于表面电离。
正离子表面电离系数 $\gamma$ :一个正离子碰撞阴极产生表面电离的电子数。
自持放电的条件是 $\gamma (\mathrm{e}^{\alpha d} - 1) \geq 1$,其中 $d$ 为极间距离。
所以,汤逊气体放电理论认为,初崩的正离子轰击阴极,产生新的电子和正离子,不断循环直到击穿。该理论的适用条件为均匀电场内、低气压、短间隙。
击穿电压与巴申理论
在均匀电场中,气体放电的击穿电压 $U_\mathrm{b}=$ 自持放电电压 $U_0$ 。
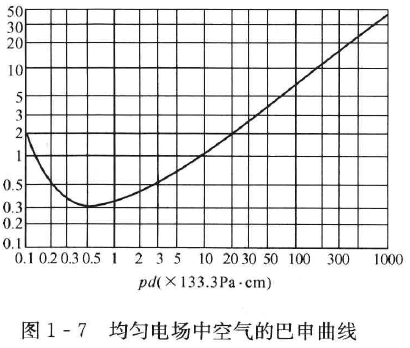
巴申理论认为,气体放电的击穿电压与极间距离和气压有关。即
该曲线呈一弯钩型,$pd$ 很大或很小时,击穿电压都会提高。这是因为在气压很小时碰撞总数少,在气压很大时电子自由行程小。
巴申定理是在温度不变的情况下得出的。在温度非恒定时,引入气体相对密度 $\delta = \frac{pT_0}{p_0T}$,则击穿电压满足
流注理论
流注理论是对汤逊气体放电理论的修正,适用于高气压和长间隙。其考虑了空间电荷对原电场的作用和空间光电离的作用。
发展过程
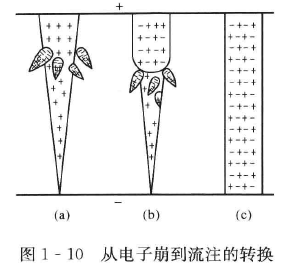
发展过程主要分四个阶段。
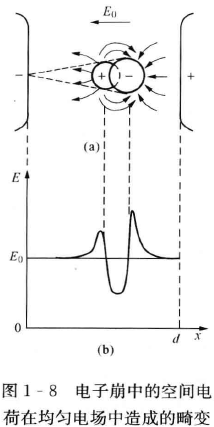
第一阶段为空间电荷畸变了外电场。电子崩头部聚集了大量正负粒子,产生了电场畸变。电场增强部分利于激励,削弱部分利于复合。强烈的复合产生大量光子,成为空间光电离辐射源。
第二阶段为二次电子崩(光电离)。
第三阶段为形成正流柱和负流柱。
主要特征
特点:电离强度大,传播速度快
出现流柱的条件也就是自持放电条件。数值上满足 $\mathrm{e}^{\alpha d} \approx10^8$ 或 $\alpha d \approx 20$ 。
适用条件
可以用于解释高气压和长间隙的放电现象。
正负流柱的区分
正流柱:初崩到阳极,再产生流柱,等离子通道从阳极生长到阴极。
负流注:初崩未到阳极就产生流柱,等离子通道从阴极或中途生长到阳极。
不均匀电场中的放电
不均匀电场中的放电与均匀电场中的放电的区别在于,均匀电场中一旦自持放电就会击穿,而不均匀电场中会出现稳定的自持放电但没有击穿的现象。
先引入电场不均匀系数
其中,$E_\mathrm{max}$ 为电场最大值,$E_\mathrm{av}$ 为电场平均值,满足
在 $1\leq f<2$ 时,放电特征与均匀电场相似。在 $f>4$ 时,场强大的空间先发生电晕放电,击穿电压比 $1\leq f<2$ 时的情况小。
电晕放电
对于一段导线,其电晕起始场强满足
其中,电晕起始场强 $E_\mathrm{c}$ 单位为 kV/cm ,$m$ 为导线表面粗糙系数,$r$ 为导线半径,$\delta$ 为空气相对密度。
使用分裂导线可以减轻电晕放电。
电晕放电会导致:电晕损耗(雨雾天气大增),无线电干扰,可闻噪声等。
极不均匀场放电的极性效应
两个原则:几何形状不同时,极性取决于曲率半径小的;几何形状相同时,极性取决于不接地的。
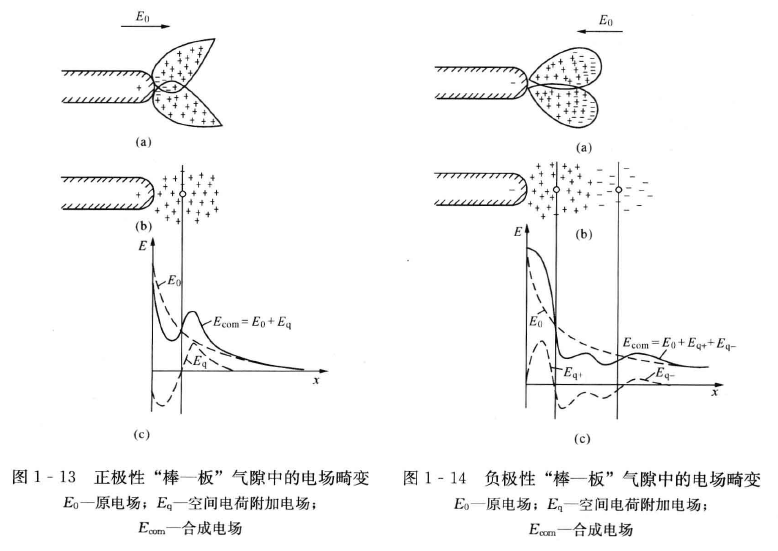
我们以“棒——板”气隙(小于 1 m)为例,来说明极性效应。
正极为棒
不容易电晕放电,但是起晕后击穿电压低。
电子崩头部的电子达到棒极后就被中和,留下了许多正离子。而正离子运动比较慢,这会削弱棒极附近的电场强度,使得电晕起始电压偏高。但是,正离子会加强粒子群后外部空间的电场。当电压进一步提高,随着电晕放电区的扩展,强场区会向板极方向推进,放电的发展是顺利的,因此击穿电压较低。
负极为棒
容易电晕放电,但是起晕后击穿电压高。
电子崩将由棒极向板极发展。由于电子速度快,棒极头部将会停留大量正离子,会加强朝向棒极端的电场强度,使得电晕起始电压偏低。但是,电子群会削弱粒子群后外部空间的电场,电晕不容易向外扩展,因此击穿电压较高。
也因此,交流电的击穿都在正半周。
长间隙极不均匀场的放电
经历三个阶段:电晕放电——先导放电——主放电。
热电离在后两个阶段有重要的作用。
先导放电就是指出现“先导通道”的放电,先导通道以热游离电子的出现作为标志。
放电时间、冲击电压和沿面放电
放电时间
放电时间的组成包括:
- $t_\mathrm{l}$: 电压从零上升到击穿电压 $U_\mathrm{s}$ 所需的时间
- $t_\mathrm{s}$: 在 $t_\mathrm{l}$ 时间后,出现第一个有效电子的时间
- $t_\mathrm{f}$: 在 $t_\mathrm{s}$ 时间后到击穿所需的时间
总时间 $t_\mathrm{b} = t_\mathrm{l} + t_\mathrm{s} + t_\mathrm{f}$ ,放电时延 $t_\mathrm{lag} = t_\mathrm{s} + t_\mathrm{f}$ 。这两个时间都具有统计性,外加电压越高,$t_\mathrm{b}$ 和 $t_\mathrm{lag}$ 越小。
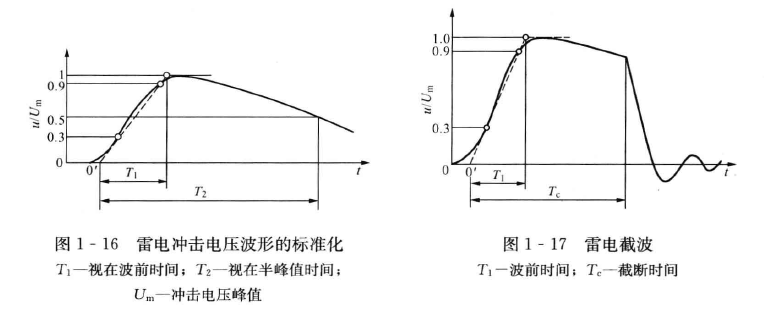
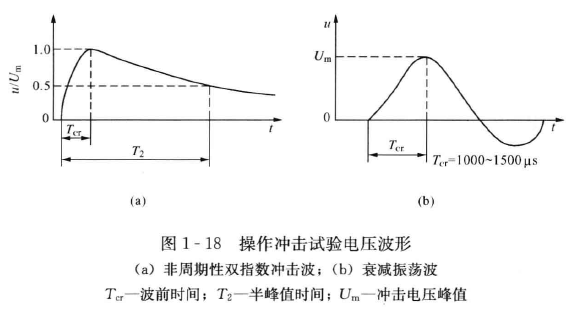
标准冲击电压
标准冲击电压包括标准雷电冲击电压波、标准雷电截波、标准操作电压冲击波。这些波形均可用冲击电压发生器产生。
50% 冲击击穿电压 $U_{50\%}$ 是指在标准冲击电压作用下,气隙击穿的概率为 50% 时的击穿电压。
冲击系数 $\beta = \frac{U_{50\%}}{U_\mathrm{s}}$ ,其中 $U_\mathrm{s}$ 为静态击穿电压。在 $f<2$ 时,$\beta\approx 1$ ;在 $f>4$ 时,$\beta>1$ 。
伏秒特性曲线的求取:保持冲击电压的波形不变,逐渐提高冲击电压的峰值。如果在电压下降时击穿则取峰值,在电压上升时击穿则取当前值,最后将这些点连成线即可。放电时间具有分散性,实际上的“曲线”为一个带状区域,我们取区域的 50% 线作为伏秒特性曲线。
若要设备 S1 能够可靠保护设备 S2,S1 的伏秒特性曲线应全面低于 S2 的伏秒特性曲线,以保证 S1 能被首先击穿。
沿面放电
沿面放电是指在两个绝缘体的界面上发生的放电现象。沿面闪络电压比气体或固体单独存在时的击穿电压都低。
沿面放电的影响因素:
- 固体绝缘材料特性:取决于材料的亲水性/憎水性
- 介质粗糙程度
- 固体介质与电极间的气隙大小
- 固体表面电场分布
套管属于有强垂直分量的极不均匀电场,支柱绝缘子属于有弱垂直分量的极不均匀电场。
表面电阻:每单位平方面积电介质表面对正方形的相对两边间表面泄露电流所产生的电阻。
滑闪放电的特征:介质表面放电通道中发生热电离。
闪络分类:
- 干闪:雷电冲击、操作冲击、运行电压都能引起
- 湿闪:操作电压、运行电压引起
- 污闪:运行电压就可引起
沿面放电电压低于气隙击穿电压的原因:
- 固体介质与电极间的缝隙会放电,畸变电场
- 大气水分在介质表面形成水膜,水膜中的粒子沿介质移动到电极,畸变电场
- 介质表面粗糙不均匀,表面电阻分散性大
减少沿面放电的方法:
- 接触面喷导电粉末
- 介质使用憎水性材料
- 改良材料
污闪过程四个阶段:积污——受潮——干区形成——局部电弧
污秽度评定:等值盐密法,单位 mg/cm² ,每平方厘米的污秽溶于水的电导等效氯化钠毫克数。
减少污闪的方法:
- 设计时增大爬电比距
- 定期清理
- 涂憎水材料
- 改良材料
介质的击穿特性
电介质的电气特性包括:导电性能、介电性能、电气强度。
电介质的主要参数:电导率 $\sigma$ 、介电常数 $\varepsilon$ 、介质损耗角正切 $\tan\delta$ 和击穿场强。
气体介质的电气特性
电气强度通常以击穿电压或击穿场强来表示。
气隙的电气强度首先取决于电场形式(均匀或不均匀),其次与外加电压的形式(工频交流电压、直流电压、雷电过电压波、操作过电压波)有关。工频交流电压和直流电压统称为稳态电压。
气隙在稳态电压作用下的击穿电压即为静态击穿电压。
空气的击穿场强约为 30 kV/cm 。
均匀电场空气间隙击穿电压可用如下经验公式来计算
其中,$U_\mathrm{b}$ 为击穿电压峰值,单位为 kV ;$d$ 为极间距离,单位为 cm ;$\delta$ 为空气相对密度。
完成气隙击穿的三个条件:
- 足够大的电压或场强
- 存在能引起电子崩并导致流柱的有效电子
- 需要一定时间(微秒级别)
细线效应:导线直径小到一定程度后,击穿电压随着直径的减小而增大。
提高电气强度的方法:
- 改善电极形状
- 利用空间电荷改善电场分布
- 采用屏障(正极性效果好,负极性会适得其反)
- 采用高气压或高真空
- 用高电气强度气体
液体与固体介质的电气特性
液体和固体介质的电气强度高于空气。
电介质的极化
介质介电常数越大,电介质极性越强,分为极性电介质、中性电介质;也跟温度和频率有关。
工频交流和冲击电压下,串联多层介质中的电场强度分布与介质相对介电常数成反比。
介质极化的分类:电子式、离子式、偶极子式、夹层和空间电荷极化。
- 电子式:存在于一切介质中,时间短,弹性位移,无能量损耗,温度的影响不大。
- 离子式:时间短,弹性位移,无能量损耗,温度的影响不大。
- 偶极子式:存在于极性分子中,时间较长,非弹性位移,有能量损耗,电场、温度的影响较大。
- 夹层介质界面极化:存在于多层介质中,暂态过程中电容略大。极化时,界面引起吸收电荷,电荷积聚的电流称为位移电流。有损耗,但只有在直流或低频下才明显。
- 空间电荷极化:时间从几秒到几十分钟不等,非弹性位移,有能量损耗,负温度系数。
电介质的电导
介质不是理想绝缘的,总会有带电粒子或空穴,在电场作用下形成传导电流(电导电流、泄漏电流)。极性电介质的电阻率要小得多。
液体电介质的电导来源于离子电导和电泳电导。
固体电介质的体积电导来源于电极中逸出的电子、介质中的离子、传到电子、空穴等。
固体电介质的表面电导来源于介质表面的污物。
电介质的能量损耗
电介质的能量损耗分为由电导引起的损耗和由极化引起的损耗。通过介质损耗可以判断绝缘材料的质量和状态。
直流电压下,损耗仅由电导引起,用体积电导和表面电导表示。交流电压下,损耗由电导和周期性极化引起,用介质损耗表示。
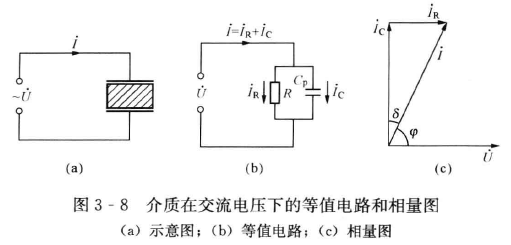
介质功率损耗
其中,$\delta$ 为介质损耗角。
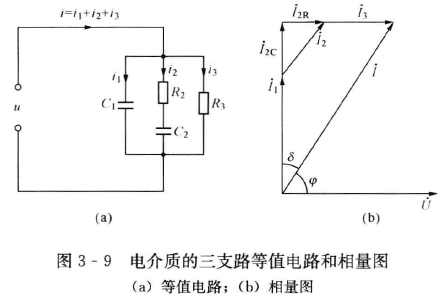
有损介质等效电路:
图中,$C_1$ 为几何尺寸决定的电容与无损极化电容之和,$C_2$ 为有损极化电容,$R_2$ 为极化过程损耗电阻,$R_3$ 为泄漏电阻。
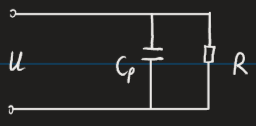
并联等值电路:
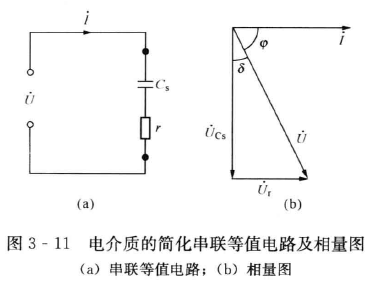
串联等值电路:
气体介质的损耗一般发生在固体、液体中含有气泡的场合。
液体介质的损耗:
- 中性、弱极性介质主要在电导上损耗
- 极性介质包括电导和极化损耗(与温度和频率有关)
固体介质的损耗:
液体介质的击穿
耐电强度一般高于气体,有绝缘、冷却、灭弧等作用。液体介质的击穿场强一般为 100-200 kV/cm 。
液体介质的击穿理论包括:
- 电击穿理论和气泡击穿理论:纯净液体电介质
- 小桥击穿理论:非纯净液体电介质
电击穿理论主要包括四个过程:电离——流柱——放电通道出现分支——贯穿间隙。类似于长间隙气体放电。
气泡击穿理论认为,液体中存在气泡,气泡中的气体电离升温,产生更多的气泡,气泡最终堆积成小桥,导致击穿。
小桥击穿理论认为,液体中存在杂质颗粒,杂质容易被极化,形成小桥,泄漏电流增大,产生更多气泡,导致击穿。液体中的杂质处于溶解或者悬浮状态。
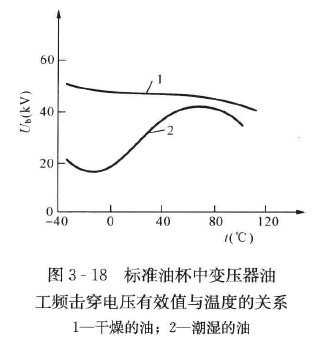
对于变压器油:
- 潮湿的油:水从悬浮到溶解,击穿电压上升;温度升高,水分汽化,击穿电压下降。
- 干燥的油:温度升高,击穿电压下降。
变压器油击穿电压的影响因素:
- 水分和其他杂质
- 油温
- 电场均匀度
- 电压作用时间
- 油压
固体介质的击穿
固体介质的耐电强度最高,击穿最复杂,是击穿后唯一不可恢复的绝缘材料。固体介质的击穿场强一般为 $10^4-10^7$ kV/cm 。
固体介质的击穿类型:电击穿、热击穿和电化学击穿。
电击穿以碰撞电离为基础。传导电子碰撞晶格,使得晶格原子电离,产生更多电子,形成电子崩,形成导电通道,导致击穿。特点是电压作用时间短,击穿电压高,温度不高;击穿场强与频率密切相关,与温度几乎无关,约为热击穿的 100 倍。
热击穿是介质的热不稳定性造成的。
电化学击穿是由于内部缺陷引起的局部放电长期作用,使得绝缘水平下降。这是因为放电产生的活性气体有氧化和腐蚀作用,此外放电产生的带电粒子撞击介质产热,有可能破坏介质分子。特征是树枝状放电,主要见于有机材料。
固体介质击穿的影响因素:
- 电压作用时间:时间短为电击穿,时间长为热击穿
- 电场均匀程度:击穿电压和厚度近似成正比
- 温度:低温为电击穿,高温为热击穿
- 受潮
- 累积效应:局部损伤会缓慢积累
电气设备绝缘试验
电力设备的可靠性与绝缘材料、绝缘结构和电气强度密切相关。绝缘材料和绝缘结构是薄弱环节,是导致事故的主要原因。
电介质理论不完善,必须依靠绝缘试验来保证设备的绝缘水平。
- 非破坏性试验:可以检测除了电气强度之外的性能,电压比较低
- 破坏性试验:主要检测电气强度,电压较高
变压器相关的实验:型式试验,出厂试验,现场试验,特殊试验。
绝缘预防性试验的目的:发现绝缘缺陷,防止事故发生。缺陷是在设备制造过程和运行过程中的外部因素导致的。
绝缘的老化
电气设备的使用寿命一般取决于绝缘的使用寿命,其与老化过程密切相关。
热老化
高温时,介质会快速老化;温度不太高但是时间长也会加速老化。
8 度法则:对于 A 级的油纸绝缘,工作温度超过规定值($105 ^\circ\mathrm{C}$)$8 ^\circ\mathrm{C}$ 时,寿命缩短约一半。
固体介质热老化的过程:固体受热导致热运动加剧,产生更多载流子,损耗增大,温度升高,形成恶性循环,最终导致击穿。
液体介质热老化的过程(油的氧化):每增高 10 度,油的氧化速度加快一倍。油在 115-120 度时开始裂解。
电老化
在高电压或强电场作用下的老化,主要原因是介质中有局部放电。
机械老化
机械应力的作用,可能会让绝缘产生裂缝。
绝缘电阻、吸收比和泄漏电流的测量
绝缘电阻 $R$ :绝缘体两端加上直流电压 $U$ 后,与流过绝缘体的泄漏电流 $I$ 的比值。
吸收比:电流衰减过程中两个瞬间(15s 和 60s)测得的两个电阻值之比,恒大于 1 。吸收比越大,绝缘性能越好。
介质损耗角正切:反映了绝缘的整体性缺陷或小电容试品的严重局部缺陷。
测量介质损耗角的影响因素:外界电磁场、温度、试验电压、试品电容量、试品表面泄露。
局部放电检测
局部放电检测是绝缘预防性试验的重要内容之一,包括视在放电量 $q$ 、放电重复率、局部放电起始电压 $U_\mathrm{s}$ 和熄灭电压 $U_\mathrm{r}$ 。
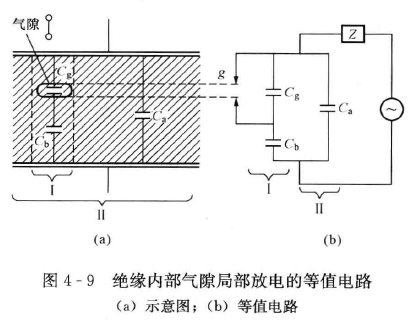
如图,假如固体或液体中存在气泡或气隙,$C_\mathrm{g}$ 为气隙的电容,$C_\mathrm{b}$ 为与气隙串联的介质电容,$C_\mathrm{a}$ 为其余完好部分的介质电容。
放电时间在微秒到纳秒级,每次放电,电压瞬时下降 $U_\mathrm{s} - U_\mathrm{r}$ ,真实放电量 $q_\mathrm{r} \approx (C_\mathrm{g}+C_\mathrm{b})(U_\mathrm{s} - U_\mathrm{r})$ ,视在放电量 $q = \frac{C_\mathrm{b}}{C_\mathrm{g}+C_\mathrm{b}}q_\mathrm{r}$ 。
其他检测方法有
- 非电方法:噪声检测法、光检测法、化学检测法
- 电方法:脉冲电流法、介质损耗法
电力系统过电压
过电压的分类
- 内部过电压
- 暂时过电压:工频电压升高、谐振过电压
- 操作过电压
- 雷电过电压
- 直接雷击过电压
- 感应雷击过电压
无损波过程
波阻抗
波速
其中 $L$ 为单位长度的电感,$C$ 为单位长度的电容。
输电线中的波
对于一根很长的输电线,电场不能认为是瞬间建立的,而是以波的形式沿线传播。电压波和电流波都是前向行波和反向行波的叠加。
记 $u’$ 和 $i’$ 分别为前向行波的电压和电流,$u’’$ 和 $i’’$ 分别为反向行波的电压和电流,则
输电线的折射与反射
过电压波在线路均匀性发生改变时的反射和折射:
- 折射系数:$\alpha=\frac{2Z_2}{Z_1+Z_2}$
- 反射系数:$\beta\frac{Z_2-Z_1}{Z_1+Z_2}$
二者的关系是 $1+\beta=\alpha$ 。
特殊的情况:
- 开路端:$Z_2 = \infty$ ,$\alpha=2$ ,$\beta=1$ ,电压翻倍,电流为零
- 短路端:$Z_2 = 0$ ,$\alpha=0$ ,$\beta=-1$ ,电压为零,电流翻倍
彼得逊法则
对于一个节点 A,假设波从一条分布参数线路传到节点 A ,并且节点 A 后连接的全部是集中参数电路(不考虑反行波),那么我们可以把线路的阻抗作为集中参数阻抗,电压波的幅值加倍,便可使用电路理论的知识计算节点 A 的电压波和电流波。
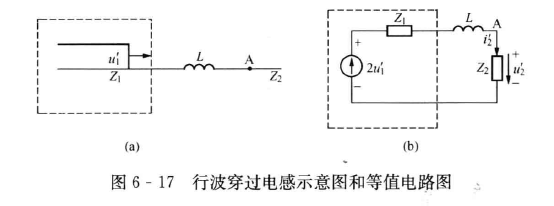
波穿过电感:
应用彼得逊法则,作出等值电路图。用 KVL 列出
用拉普拉斯变换解出来
其中,$ \tau_{\scriptscriptstyle\mathrm{L}} = \frac{L}{Z_1+Z_2} $ 为回路的时间常数,$\alpha = \frac{2Z_2}{Z_1+Z_2}$ 为没有电感时的电压折射系数。
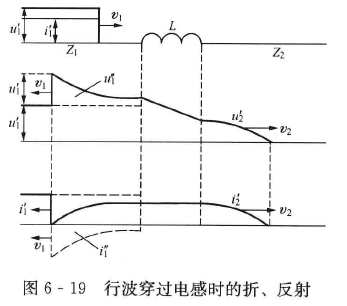
波前陡度为
电流反射波用 $i_1’’=i_2’-i_1’$ 计算即可,电压反射波用 $u_1’’=-Z_1i_1’’$ 计算即可。
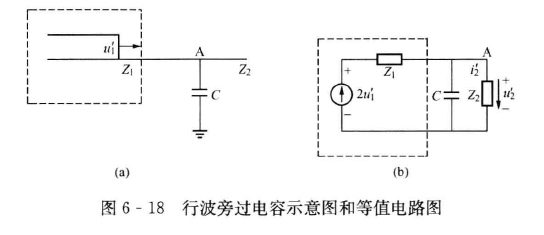
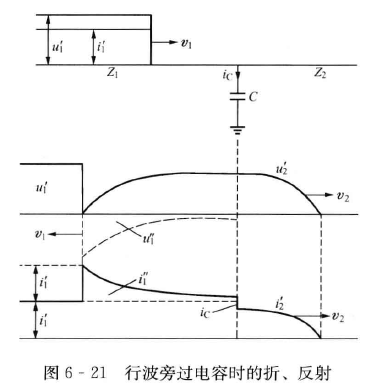
波旁过电容:
应用彼得逊法则,作出等值电路图。列出方程
用拉普拉斯变换解出来
其中,$\tau_{\scriptscriptstyle\mathrm{C}} = \frac{Z_1Z_2}{Z_1+Z_2}C$ 为回路的时间常数,$\alpha = \frac{2Z_2}{Z_1+Z_2}$ 为没有电容时的电压折射系数。
波前陡度为
电压反射波用 $u_1’’=u_2’-u_1’$ 计算即可,电流反射波用 $i_1’’=-\displaystyle\frac{u_1’’}{Z_1}$ 计算即可。