电力电子技术

第一章 绪论

电力电子技术是在电子、电力和控制技术基础上发展起来的新兴学科。

电力电子技术的三要素是：器件、拓扑和控制。

根据电能的输入——输出形式来分，主要包含以下四种基本变换

1. AC-DC变换: 整流器
2. DC-AC变换: 逆变器
3. DC-DC变换: 直流变换器、斩波器
4. AC-AC变换: 交流变换器、周波变流器

第二章 电力电子器件

电力电子器件的概念和特征

电力电子器件具有以下特点：

1. 处理功率大
2. 工作在开关状态
3. 需要控制电路
4. 需要驱动电路
5. 功率损耗大

电力电子器件的功率损耗主要包括通态损耗、断态损耗和开关损耗，其中开关损耗又包括开通损耗和关断损耗。

电力电子器件的分类

电力电子器件通常按照能够被控制电路信号所控制的程度分为：

1. 不可控器件：功率二极管
2. 半控型器件：晶闸管 SCR
3. 全控型器件：电力晶体管 GTR，门极可关断晶闸管 GTO，电力场效应管 MOSFET 等

按照控制电路加在电力电子器件控制端和公共端之间信号的性质，全控型器件又可分为电流型和电压型。

根据器件内部导电粒子的性质，全控型器件又可分为单极型、双极型和复合型。器件内部只有一种导电粒子的称为单极型器件，如电力场效应管；具有两种导电粒子的称为双极型器件，如电力三极管；由单极型和双极型复合成的器件称为复合型器件，如绝缘栅双极晶体管 IGBT。

电力电子器件基础

实际上，这一部分在模拟电子技术中已经学习过，但在电力电子技术中，会有更多的补充知识，因此这里再次详细叙述一遍。

PN 结

完全纯净的、结构完整的半导体晶体称为本征半导体；在掺入杂质后，形成的半导体称为杂质半导体。在掺杂后，会引入多子，同时由于热激发，会产生少量少子。

载流子因为热运动而从高浓度区向低浓度区的扩散称为扩散运动，而由于电场的作用使载流子运动称为漂移运动。内电场的增强会削弱扩散运动，增强漂移运动。

当 P 型半导体和 N 型半导体接触时，P 型半导体中的多子（空穴）会向 N 型半导体扩散，而 N 型半导体中的多子（电子）会向 P 型半导体扩散。由于两种载流子在接触面处的复合，形成了一个电荷中性区，称为空间电荷区。

PN 结包含三种反向击穿形式：雪崩击穿（高电压）、齐纳击穿（高掺杂）和热击穿。

PN 结包含势垒电容和扩散电容（存储电容）。

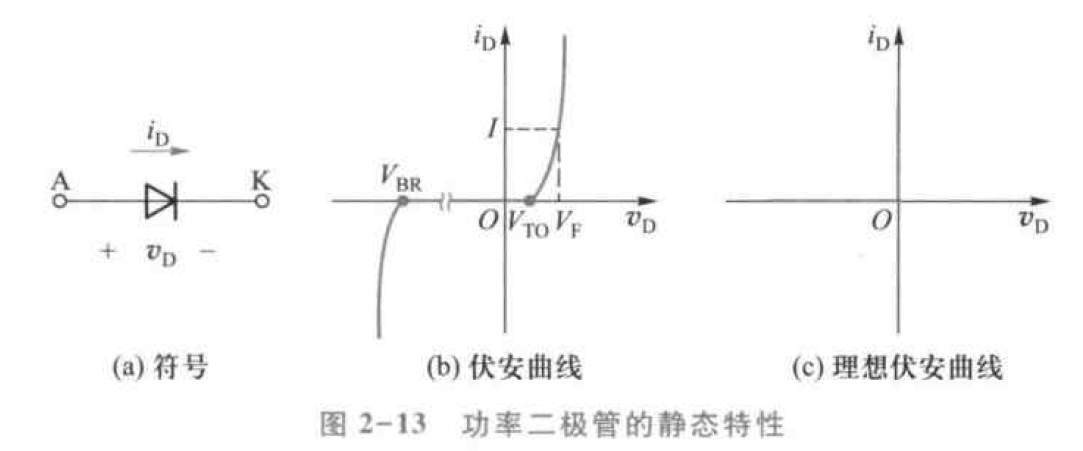
不可控器件——功率二极管

功率二极管有三种典型应用：整流、续流、钳位。

基本结构与工作原理

功率二极管本质也是 PN 结，但由于其结构和材料的不同，具有更大的电流和电压承受能力。功率二极管与信息电子二极管相比，具有以下特点：

1. 功率二极管体积更大
2. 功率二极管大都是垂直导电结构
3. 功率二极管在 P 区和 N 区之间多了一层低掺杂 N- 区，因此功率二极管的结构也被称为 P-i-N 结构

由于电导调制效应，功率二极管尽管有低掺杂区，其正向压降仍然较小。

功率二极管是负温度系数的，即温度升高时，电阻减小。

静态特性

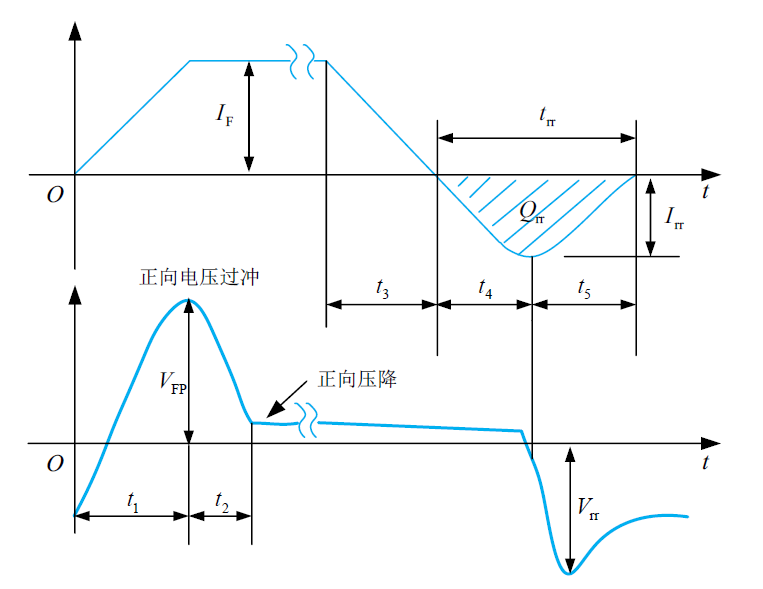
动态特性

由正向偏置转为反向偏置后，功率二极管并不能立即关断，而是会有一个反向恢复过程。图中 $t_3$ 末期，电流下降为零，但是由于功率二极管的空间电荷区两侧（特别是多掺杂 N 区）储存有大量少子，在外加电压的作用下被抽出二极管，流过较大的反向电流。由于寄生电感的作用，二极管将产生很大的反向电压 $V_\mathrm{rr}$ 。

定义如下重要参数：

1. 延迟时间 $t_\mathrm{d}=t_4$：从反向恢复电流开始上升到反向恢复电流到达最大的时间。
2. 电流下降时间 $t_\mathrm{f}=t_5$：从反向恢复电流到达最大到反向恢复电流下降到零的时间。
3. 反向恢复时间 $t_\mathrm{rr}=t_\mathrm{d}+t_\mathrm{f}$：从反向恢复电流开始上升到反向恢复电流下降到零的时间。
4. 恢复特性的软度（恢复系数） $S_\mathrm{r}=\frac{t_\mathrm{f}}{t_\mathrm{d}}$：恢复系数越大，恢复性能越软，尖峰、振荡越小。

由反向偏置到正向偏置时，功率二极管也会有一个正向恢复过程。出现电压过冲的原因是电导调制效应起作用需要一定时间。

肖特基二极管

肖特基二极管是由金属和 N 型半导体接触形成的 PN 结，具有以下特点：

1. 多子导电的单极性器件
2. 反向恢复时间极短
3. 损耗小
4. 反向耐压能力弱

二极管的主要类型

1. 普通二极管

   又称为整流二极管，适用于开关频率不高 (1 kHz 以下) 的场合，反向恢复时间长。

2. 快恢复二极管

   适用于开关频率较高 (1 kHz 至 10 kHz) 的场合，反向恢复时间短。多用于 DC-DC 电路。

3. 肖特基二极管

   属于多子器件，反向恢复时间极短，正向恢复过程中也不会有明显的电压过冲。

半控型器件——晶闸管

适用于大功率、低开关频率场合。

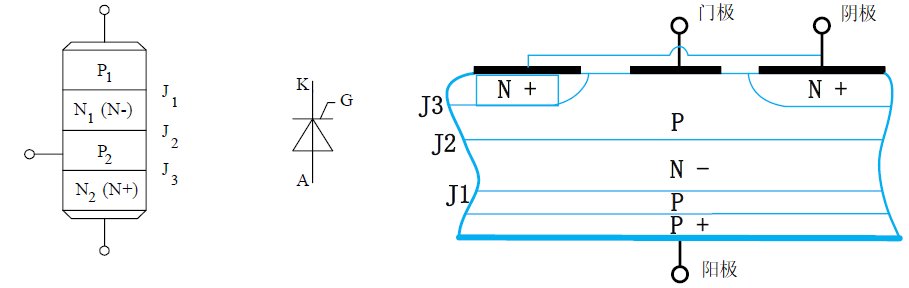
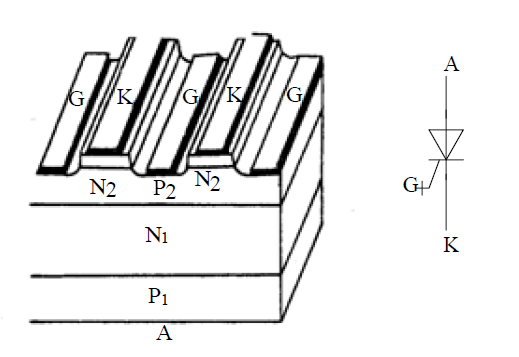
基本结构与工作原理

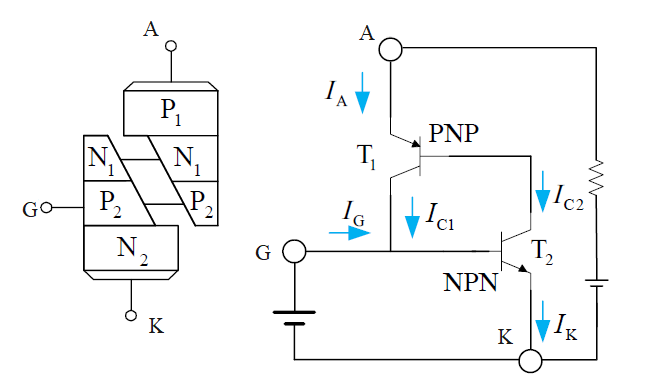
晶闸管是三端四层结构，具有 P-N-P-N 结构。如果把晶闸管斜切一刀，则可以看做 PNP 和 NPN 两个三极管的组合。

如图，当 G 极加上电压后，三极管 $T_2$ 导通，$T_1$ 也会导通。此时正反馈形成，即使去掉 G 极的电压，晶闸管仍然会导通。我们可以列出如下方程

$$\begin{cases} I_\mathrm{C1}=\alpha_1 I_\mathrm{A} + I_\mathrm{CBO1} \\ \\ I_\mathrm{C2}=\alpha_2 I_\mathrm{K} + I_\mathrm{CBO2} \\ \\ I_\mathrm{K}=I_\mathrm{A}+I_\mathrm{G} \\ \\ I_\mathrm{A}=I_\mathrm{C1}+I_\mathrm{C2} \end{cases}$$

其中，$\alpha_1$ 和 $\alpha_2$ 分别是 $T_1$ 和 $T_2$ 的共基极电流增益；$I_\mathrm{CBO1}$ 和 $I_\mathrm{CBO2}$ 分别是 $T_1$ 和 $T_2$ 的共基极漏电流。由此可以解得

$$I_\mathrm{A}=\frac{\alpha_2I_\mathrm{G}+I_\mathrm{CBO1}+I_\mathrm{CBO2}}{1-(\alpha_1+\alpha_2)}$$

所以，导通时有 $ \alpha_1+\alpha_2 \approx 1 $ 。

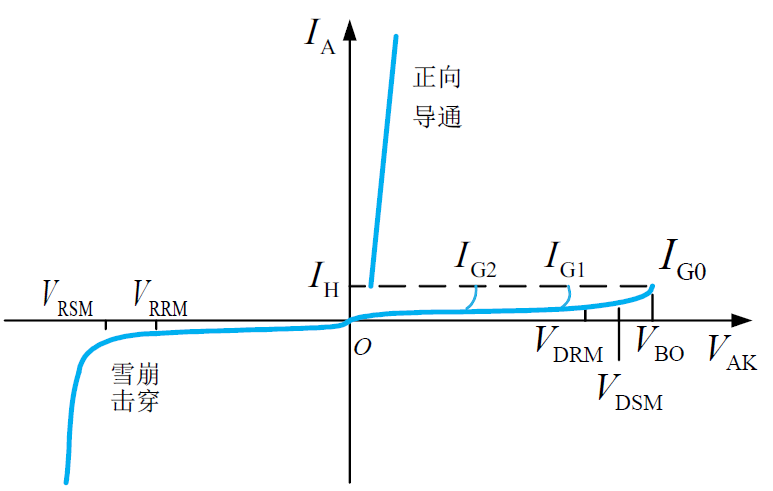
静态特性

图中，$V_\mathrm{DRM}$, $V_\mathrm{RRM}$ 是晶闸管的正反向断态重复峰值电压；$V_\mathrm{DSM}$, $V_\mathrm{RSM}$ 是晶闸管的正反向断态不重复峰值电压；$V_\mathrm{BO}$ 是晶闸管的正向转折电压；$I_\mathrm{H}$ 是晶闸管的维持电流。

晶闸管的额定电压是正反向断态重复峰值电压 $V_\mathrm{DRM}$ 和 $V_\mathrm{RRM}$ 中的较小值。

维持电流是指使晶闸管维持导通的最小电流。另一个概念是擎住电流 $I_\mathrm{L}$，是指使晶闸管从关断状态转为导通状态并移除触发信号的最小电流，一般为维持电流的 2~4 倍。

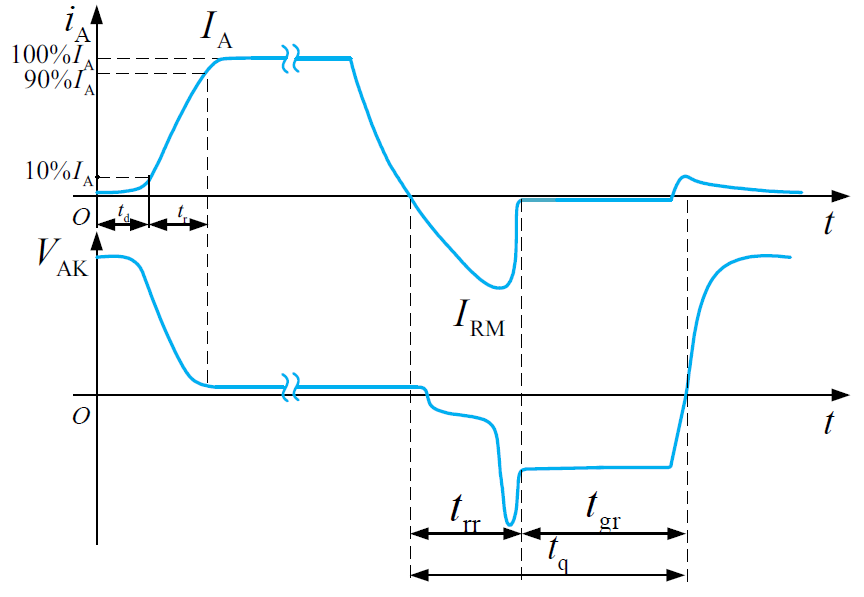
动态特性

图中，$t_\mathrm{d}$ 是延迟时间，指从门极电流阶跃时刻开始，到阳极电流上升到稳态值的 10% 的时间；$t_\mathrm{r}$ 是上升时间，指从阳极电流从稳态值的 10% 上升到稳态值的 90% 的时间；开通时间 $t_\mathrm{on}=t_\mathrm{d}+t_\mathrm{r}$ 。

$t_\mathrm{rr}$ 是反向阻断恢复时间，指从正向电流下降到零到反向电流下降到零的时间；$t_\mathrm{gr}$ 是正向阻断恢复时间，在反向恢复过程结束后，由于载流子的复合过程比较慢（PN 结中的少子难以通过外电路抽取），晶闸管恢复正向阻断电压的能力需要一定时间。关断时间 $t_\mathrm{off}=t_\mathrm{rr}+t_\mathrm{gr}$ 。

全控型器件——门极可关断晶闸管

门极可关断晶闸管拥有晶闸管全部的优点，同时可以通过门极施加负的脉冲信号关断。

基本结构与工作原理

在晶闸管一章，我们已经学习到，导通电流 $I_\mathrm{A}=\displaystyle\frac{\alpha_2I_\mathrm{G}+I_\mathrm{CBO1}+I_\mathrm{CBO2}}{1-(\alpha_1+\alpha_2)}$。而 GTO 具有以下特点，使其能够自主关断：

1. 设计 $\alpha_2$ 较大，使晶体管 $T_2$ 控制灵敏
2. 导通后 $\alpha_1+\alpha_2$ 更接近于 1

当然，这样的设计也导致了其管压降比较大。

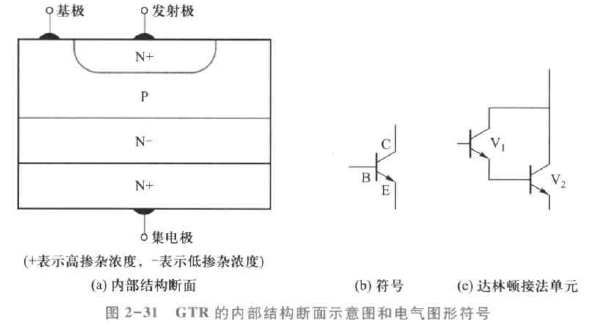
全控型器件——电力晶体管

基本结构与工作原理

电力晶体管比普通三极管能够承受更高的电压，这是因为其在普通三极管的基础上增加了低掺杂 N- 层。

全控型器件——电力场效应晶体管

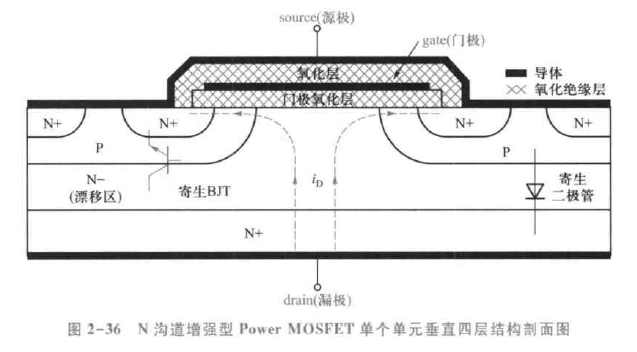
电力场效应晶体管分为结型 JFET 和绝缘栅型 MOSFET 两种，都是多子导电型器件。一般而言我们很少用到结型场效应管，所以后文我们以 MOSFET 的学习为主。MOSFET 具有四层结构 N+, P, N-, N+ 。

基本结构与工作原理

MOSFET 具有正温度系数，易于并联。

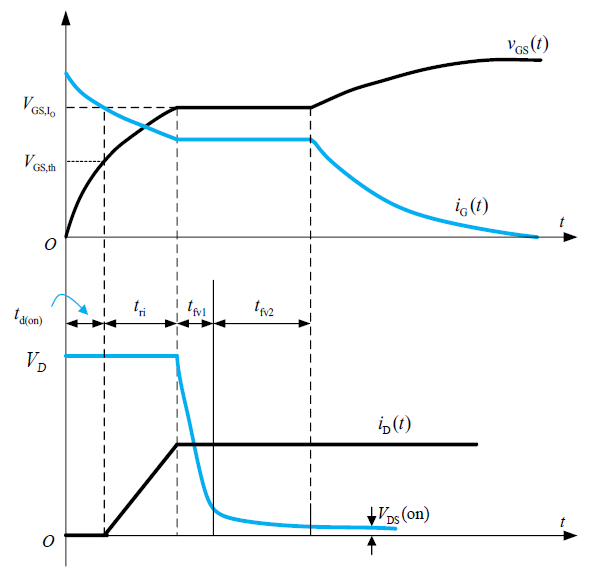
动态特性

这里只介绍米勒平台的形成。

第一阶段，$t_\mathrm{d}$ 时段，此阶段对 $C_\mathrm{GS}$ 和 $C_\mathrm{GD}$ 两个电容充电。$V_\mathrm{D}$ 保持不变，所以主要考虑对 $C_\mathrm{GS}$ 的充电直至其达到开启电压 $V_\mathrm{GS,th}$（大约2-3V），从而结束该阶段。

第二阶段，$t_\mathrm{ri}$ 时段，该阶段开始已经达到门极开启电压，$i_\mathrm{D}$ 在此时段开始上升。从二极管到 MOSFET 的换流开始，因为换流结束前二极管仍然有电流，所以 $V_\mathrm{D}$ 仍然被钳位在直流电压。

第三阶段，$t_\mathrm{fv1}$ 时段，该阶段开始时，$i_\mathrm{D}$ 刚达到满载电流，则二极管关断，不再钳位 $V_\mathrm{D}$ 。此时在门极驱动电路对 $C_\mathrm{GD}$ 反向充电作用下，$V_\mathrm{DS}$ 开始快速下降。同时因为 $i_\mathrm{D}$ 已经达到满载电流不变，受跨导曲线的约束，$V_\mathrm{GS}$ 必定不变。综上两个原因，可以认为驱动电路几乎只对 $C_\mathrm{GD}$ 充电，而不再对 $C_\mathrm{GS}$ 充电，$V_\mathrm{GS}$ 不变而形成一个平台，称为米勒平台。

特征总结

1. MOSFET 的开关速度和其输入电容的充放电有很大关系
2. 多子导电，开关速度快
3. 开关时间短，工作频率是主要电力电子器件中最高的
4. 多子导电，没有电导调制效应，饱和导通后会等效成一个电阻
5. 多用于电压较低的场合
6. 具有正温度系数，易于并联，没有二次击穿现象

全控型器件——绝缘栅双极晶体管

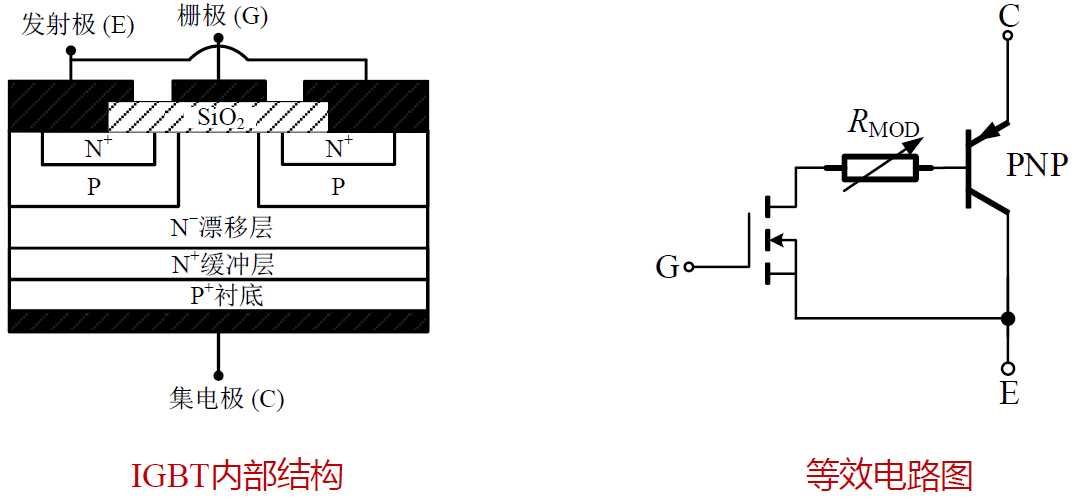
绝缘栅双极晶体管（IGBT）是 MOSFET 和 GTO 的结合体，具有 MOSFET 的高输入阻抗和 GTO 的高电流密度。IGBT 具有五层结构 N+, P, N-, N+, P 。

基本结构与工作原理

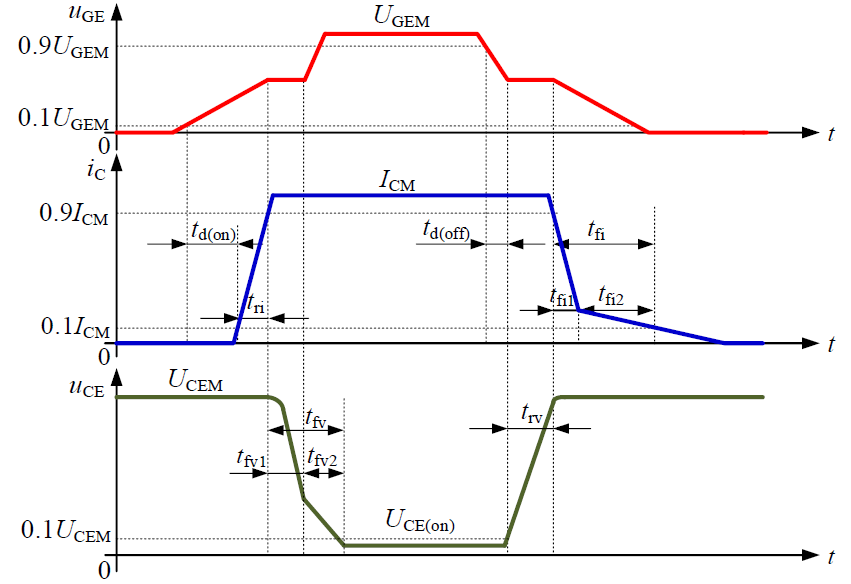
动态特性

这里只介绍电流拖尾效应。

图中，$t_\mathrm{fi1}$ 对应 IGBT 内部 MOSFET 和 GTR 一起的关断过程，这段时间集电极电流 $i_\mathrm{C}$ 下降较快。$t_\mathrm{fi2}$ 对应 IGBT 内部 PNP 晶体管的关断过程，这段时间内因为 MOSFET 已经关断，晶体管无基区少子抽取通道，所以晶体管 N 基区内的少子复合缓慢，造成 $i_\mathrm{C}$ 下降较慢，这称为 IGBT 的电流拖尾现象。

本章的最后，放一个电力电子器件的对比表格：

器件	功率	开关速度	电压等级
电力晶体管 GTR	中	中	中
门极可关断晶闸管 GTO	高	慢	高
电力场效应管 MOSFET	低	快	低
绝缘栅双极晶体管 IGBT	中	中	高

第三章 前置知识

变换器的开关模式控制

各种变换器主要有两种变换模式：脉冲频率调制 (PFM) 和脉冲宽度调制 (PWM) 。PFM 通过改变开关频率来改变输出电压，而 PWM 则通过改变开关的占空比来改变输出电压。现在 PFM 很少使用，PWM 为主流的控制方式。

为了得到占空比可调的 PWM 信号，我们会设置一个锯齿波 $v_{\scriptscriptstyle\mathrm{ST}}$ （称为载波） 和控制电压 $v_\mathrm{control}$ （称为调制波），当 $v_\mathrm{control}$ 大于 $v_{\scriptscriptstyle\mathrm{ST}}$ 时，输出高电平，否则输出低电平。这样我们只需要控制 $v_\mathrm{control}$ 的大小，就可以控制输出占空比。

非正弦周期波形分析

非正弦周期波形可以通过傅里叶级数展开为一系列正弦波的叠加。对于周期为 $T$ 的非正弦周期波形 $i_\mathrm{s}(t)$，使用傅里叶级数展开，可以得到基波 $i_\mathrm{s1}$ 和高次谐波 $i_{\mathrm{s}h}$ 。

电流有效值为

$$I_s=\sqrt{\frac{1}{T}\int_0^T i_s^2(t)dt} = \sqrt{I_\mathrm{s1}^2+\sum_{h \ne 1}I_{\mathrm{s}h}^2}$$

畸变分量为

$$i_\mathrm{dis} = i_\mathrm{s}(t) - i_\mathrm{s1}(t) = \sum_{h \ne 1}i_{\mathrm{s}h}(t)$$

畸变分量有效值为

$$I_\mathrm{dis} = \sqrt{\sum_{h \ne 1}I_{\mathrm{s}h}^2}$$

总谐波畸变率为

$${THD} = \frac{I_\mathrm{dis}}{I_\mathrm{s1}} = \frac{\sqrt{I_\mathrm{s}^2-I_\mathrm{s1}^2}}{I_\mathrm{s1}}$$

假如输入电压为标准正弦波，则平均功率为

$$P=\frac{1}{T}\int_0^T v_\mathrm{s}(t)i_\mathrm{s}(t)dt = V_\mathrm{s}I_\mathrm{s1}\cos\varphi$$

功率因数为

$${PF} = \frac{P}{V_\mathrm{s}I_\mathrm{s}} = \frac{I_\mathrm{s1}}{I_\mathrm{s}}\cos\varphi = k_\mathrm{d}\cos\varphi = \frac{1}{\sqrt{1+{THD}^2}}{DPF}$$

其中，$k_\mathrm{d}=\displaystyle\frac{I_\mathrm{s1}}{I_\mathrm{s}}$ 是畸变因数，$\cos\varphi$ 是相移功率因数 DPF。

伏秒平衡与安秒平衡

伏秒平衡是指处于稳定状态的电感，在一个周期内，电压的平均值为 0.

安秒平衡是指处于稳定状态的电容，在一个周期内，电流的平均值为 0.

实际上就是电荷守恒和磁链守恒。

第四章 DC-DC 变换器

DC-DC 变换器的典型应用有：开关电源、充电器、电机驱动器等，按照输入与输出间是否有电气间隔可分为隔离型和非隔离型。

非隔离型 DC-DC 变换器按照所用的有源功率器件的个数，可以分为单管、双管和四管三类。单管 DC-DC 变换器主要有降压型 (Buck)、升压型 (Boost)、降升压型 (Buck-Boost)、Cuk 变换器、Zeta 变换器和 Sepic 变换器。

单管隔离型 DC-DC 变换器主要有正激式 (Forward)、反激式 (Flyback) 两种。双管隔离型 DC-DC 变换器主要有双管正激、双管反激、推挽式、半桥式四种。

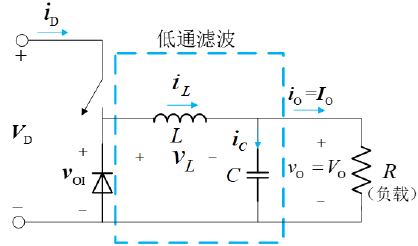
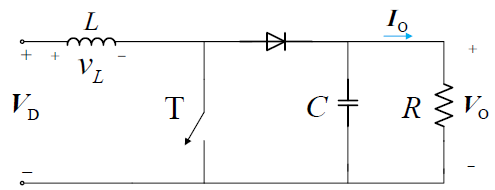
降压式变换器

Buck 变换器有两种工作模式，即连续导通模式 (CCM) 和断续导通模式 (DCM)。这两种工作方式之间有一个边界，称为临界导通模式。这里只介绍连续导通模式。

连续导通模式分析

在分析时，由于电容的作用，输出电压 $V_\mathrm{O}$ 可以看做是一个常数。

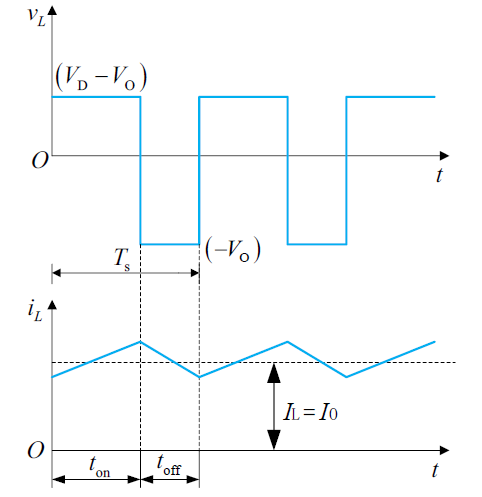
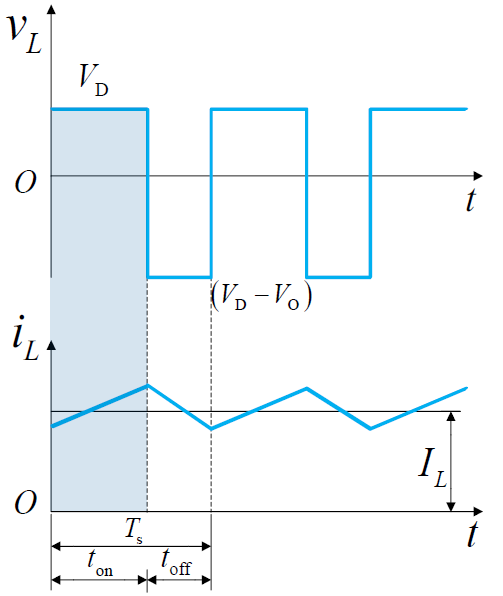
开关导通时，电感充电，电感电流成线性上升

$$i_\mathrm{L}(t)=\frac{V_\mathrm{D}-V_\mathrm{O}}{L}t + i_\mathrm{L}(0)$$

当 $t=t_\mathrm{on}$ 时，电感电流达到最大值 $i_\mathrm{L, peak}$。

开关关断时，电感通过二极管放电，电感电流成线性下降

$$i_\mathrm{L}(t)= -\frac{V_\mathrm{O}}{L}(t-t_\mathrm{on}) + i_\mathrm{L, peak}$$

由伏秒平衡可以得到

$$(V_\mathrm{D}-V_\mathrm{O})t_\mathrm{on} = V_\mathrm{O}t_\mathrm{off}$$

化简得到

$$\frac{V_\mathrm{O}}{V_\mathrm{D}}=D$$

如果忽略功率损耗，则有

$$\frac{I_\mathrm{O}}{I_\mathrm{D}}=\frac{1}{D}$$

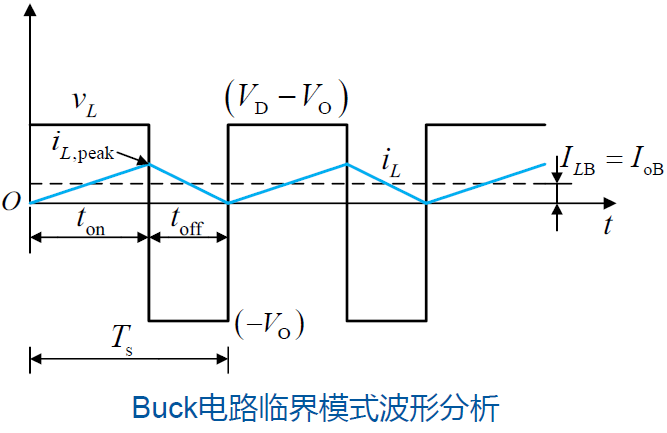
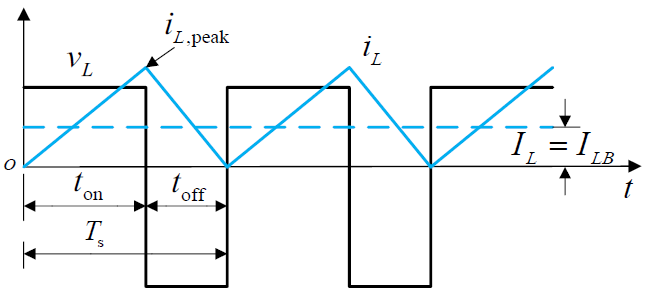
在临界模式下，电感电流平均值为

$$I_\mathrm{LB} = \frac{1}{2}i_\mathrm{L, peak} = \frac{V_\mathrm{D}-V_\mathrm{O}}{2L}t_\mathrm{on} = \frac{DT_\mathrm{s}}{2L}(V_\mathrm{D}-V_\mathrm{O}) = I_\mathrm{OB}$$

如果输入电压为常数，则有

$$I_\mathrm{LB} = \frac{V_\mathrm{D}T_\mathrm{s}}{2L}D(1-D)$$

$D$ 为变量，可以求出抛物线最大值。

如果输出电压为常数，则有

$$I_\mathrm{LB} = \frac{V_\mathrm{O}T_\mathrm{s}}{2L}(1-D)$$

在给定的 $D$ 下，如果输出电流平均值大于等于 $I_\mathrm{LB}$，则工作在连续导通模式；如果小于 $I_\mathrm{LB}$，则工作在断续导通模式。

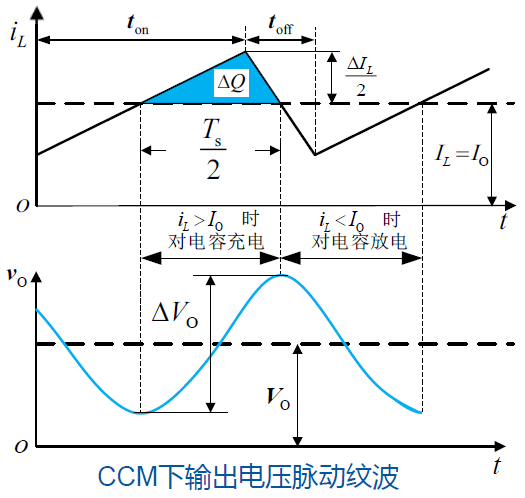
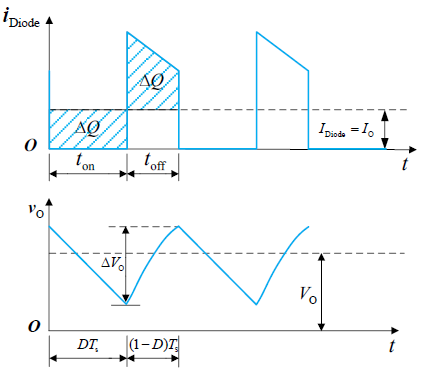
输出电压纹波脉动分析

实际上，当电容有限时，输出电流和电压都有纹波。为了定量计算输出电压的纹波成分，我们假设负载电流为定值，此时电感电流的平均值与之相等。当电感电流大于平均值时，电容充电，反之放电。

电容在一个开关周期内的充电电荷为

$$\Delta Q = \frac{1}{2}\cdot \frac{\Delta I_\mathrm{L}}{2}\cdot \frac{T_\mathrm{s}}{2}$$

在上面，我们已经推导了 $\Delta I_\mathrm{L}=\displaystyle\frac{V_\mathrm{O}}{L}(1-D)T_\mathrm{s}$，则脉动电压为

$$\Delta V_\mathrm{O} = \frac{\Delta Q}{C} = \frac{T_\mathrm{s}}{8C}\cdot \frac{V_\mathrm{O}}{L}(1-D)T_\mathrm{s}$$

纹波率为

$$\frac{\Delta V_\mathrm{O}}{V_\mathrm{O}} = \frac{T_\mathrm{s}^2}{8}\cdot \frac{1-D}{LC} = \frac{\pi^2}{2}(1-D)\left(\frac{f_\mathrm{c}}{f_\mathrm{s}}\right)^2$$

其中，$f_\mathrm{c}=\displaystyle\frac{1}{2\pi \sqrt{LC}}$

升压式变换器

同样，Boost 变换器也有两种工作模式。这里只介绍连续导通模式。

连续导通模式分析

在分析时，由于电容的作用，输出电压 $V_\mathrm{O}$ 可以看做是一个常数。

开关导通时，电感充电，电感电流成线性上升

$$i_\mathrm{L}(t)=\frac{V_\mathrm{D}}{L}t + i_\mathrm{L}(0)$$

当 $t=t_\mathrm{on}$ 时，电感电流达到最大值 $i_\mathrm{L, peak}$。

开关关断时，电感通过二极管放电，电感电流成线性下降

$$i_\mathrm{L}(t)= \frac{V_\mathrm{D}-V_\mathrm{O}}{L}(t-t_\mathrm{on}) + i_\mathrm{L, peak}$$

由伏秒平衡可以得到

$$V_\mathrm{D}t_\mathrm{on} = (V_\mathrm{O}-V_\mathrm{D})t_\mathrm{off}$$

化简得到

$$\frac{V_\mathrm{O}}{V_\mathrm{D}}=\frac{1}{1-D}$$

如果忽略功率损耗，则有

$$\frac{I_\mathrm{O}}{I_\mathrm{D}}=1-D$$

在临界模式下，电感电流平均值为

$$I_\mathrm{LB} = \frac{1}{2}i_\mathrm{L, peak} = \frac{V_\mathrm{D}}{2L}t_\mathrm{on} = \frac{T_\mathrm{s}V_\mathrm{O}}{2L}D(1-D)$$

电感的平均电流与输入平均电流相等，则输出电流满足

$$I_\mathrm{OB} = (1-D)I_\mathrm{LB} = \frac{V_\mathrm{O}T_\mathrm{s}}{2L}D(1-D)^2$$

同样，可以用不等式求出输入电流平均值或输出电流平均值最大值。

在给定的 $D$ 下，如果输出电流平均值大于等于 $I_\mathrm{OB}$，则工作在连续导通模式；如果小于 $I_\mathrm{OB}$，则工作在断续导通模式。

输出电压纹波脉动分析

以连续导通模式为例，输出电压纹波脉动分析与降压式变换器类似。这里我们假设在 $t_\mathrm{off}$ 末端时，二极管电流仍然大于输出平均电流 $I_\mathrm{O}$ ，否则计算会变得比较复杂。

在一个周期内，电容的充电电荷为

$$\Delta Q = I_\mathrm{O}DT_\mathrm{s}$$

纹波电压为

$$\Delta V_\mathrm{O} = \frac{\Delta Q}{C} = \frac{I_\mathrm{O}DT_\mathrm{s}}{C}$$

假如为纯阻性负载，则有

$$\Delta V_\mathrm{O} = \frac{V_\mathrm{O}DT_\mathrm{s}}{RC}$$

纹波率为

$$\frac{\Delta V_\mathrm{O}}{V_\mathrm{O}} = \frac{DT_\mathrm{s}}{RC} = \frac{DT_\mathrm{s}}{\tau}$$

如果 $\tau$ 比较大，那么可以忽略纹波。

升降压变换器

升降压变换器的分析与前文并无什么不同，这里只给出结论。

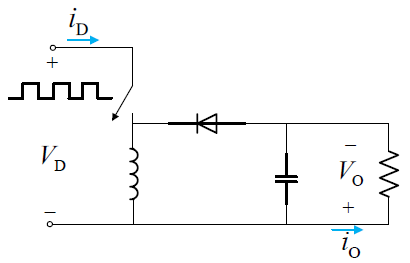
注意，升降压变换器的输出电压 $V_\mathrm{O}$ 的极性与输入电压 $V_\mathrm{D}$ 的极性相反。

用伏秒平衡可以得到

$$\frac{I_\mathrm{D}}{I_\mathrm{O}}=\frac{V_\mathrm{O}}{V_\mathrm{D}}=\frac{D}{1-D}$$

输入电流、输出电流和电感电流平均值之间的关系为

$$I_\mathrm{O} = I_\mathrm{L} - I_\mathrm{D}$$

用这个关系去算临界模式导通即可。

纹波分析与 Boost 变换器完全一致（实际上从输出端看就是个 Boost 变换器）。

纹波电压

$$\Delta V_\mathrm{O} = \frac{I_\mathrm{O}DT_\mathrm{s}}{C} = \frac{V_\mathrm{O}DT_\mathrm{s}}{RC}$$

纹波率

$$\frac{\Delta V_\mathrm{O}}{V_\mathrm{O}} = \frac{DT_\mathrm{s}}{RC}$$

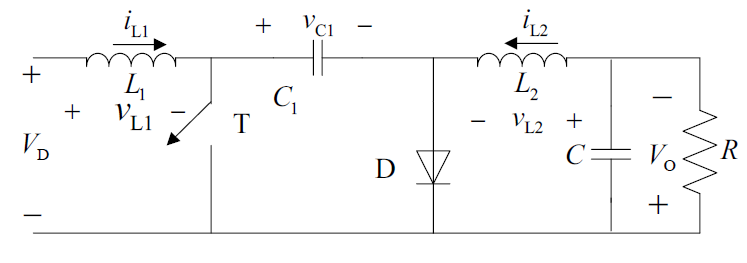
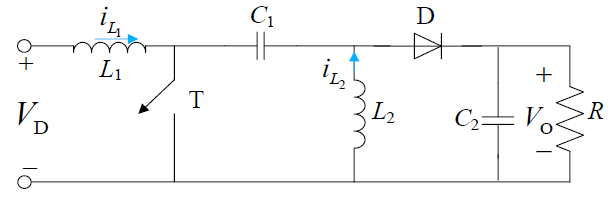
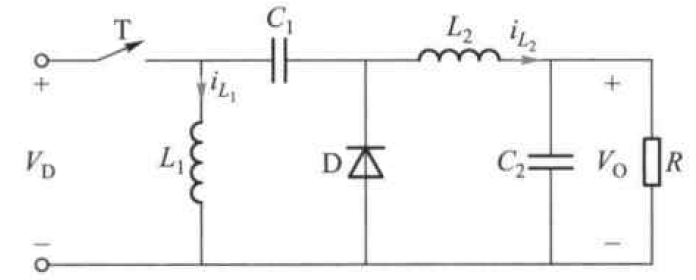
Cuk, Sepic 和 Zeta 变换器

这里面只有 Cuk 变换器的输出电压极性与输入电压相反。

单端正激变换器

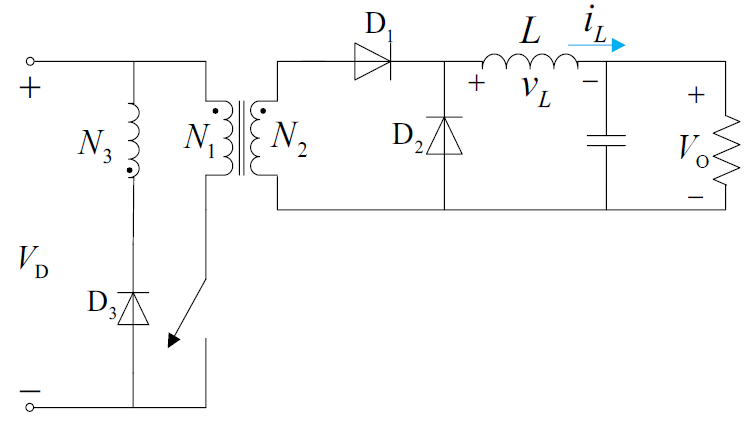
Forward 变换器是在 Buck 变换器的续流二极管前增加了一个变压器，再增加一个整流二极管组成的。

正激的含义：隔离变压器初级线圈连接的 MOS 管在导通时，变压器次级形成整流过程，在 MOS 管关断时进行磁复位。

正激变换器有如下特点:

1. 变压器同名端在同一位置
2. 需要磁复位
3. 需要整流二极管
4. 输出电压极性与输入电压相同

如果不进行磁复位，那么变压器一次侧的磁链会不断增大直到饱和，导致无法输出电压。

输入电压与输出电压之间的关系为

$$\frac{V_\mathrm{O}}{V_\mathrm{D}} = \frac{N_\mathrm{2}}{N_\mathrm{1}}D$$

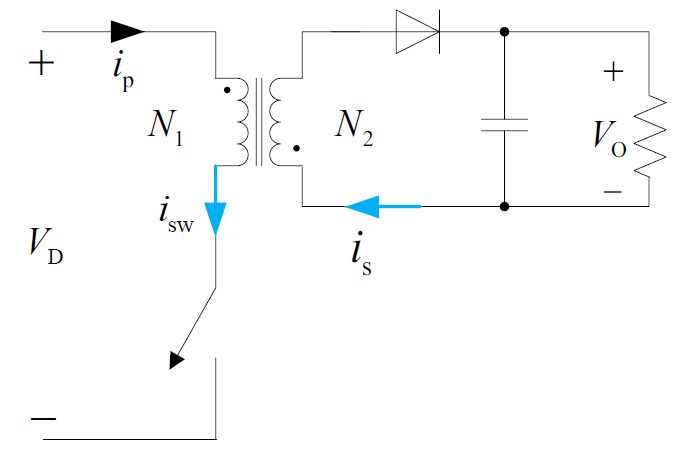
单端反激变换器

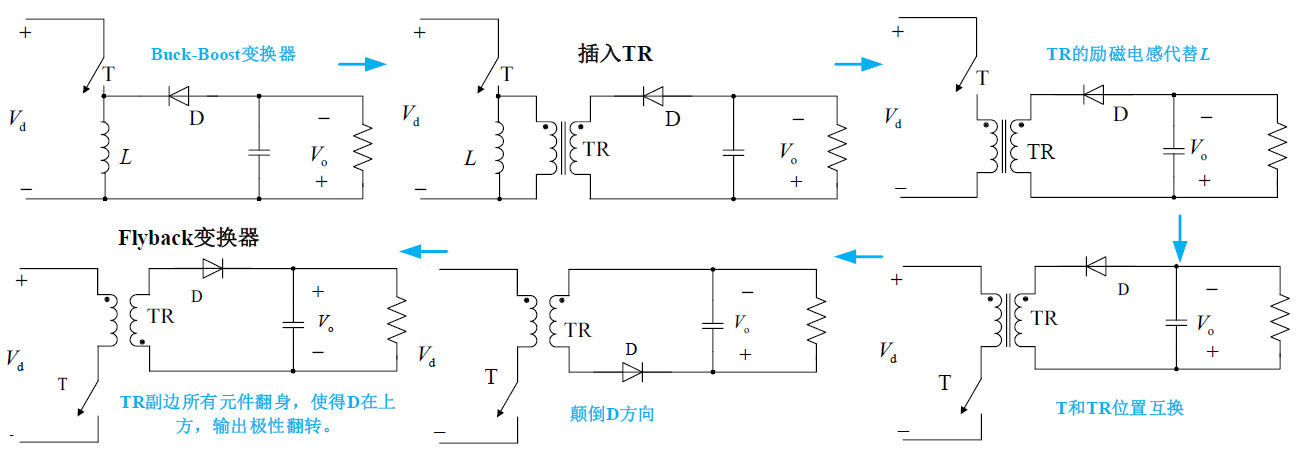
Flyback 变换器是由 Buck-Boost 变换器插入变压器演化出来的。

反激的含义：隔离变压器初级线圈连接的 MOS 管在关断时，变压器次级形成整流过程，同时进行磁复位。

反激变换器有如下特点:

1. 变压器同名端在不同位置
2. 不需要磁复位，但需要留出气隙防止饱和
3. 需要假负载给电容放电
4. 输出电压极性与输入电压相同
5. 效率比正激变换器低

输入电压与输出电压之间的关系为

$$\frac{V_\mathrm{O}}{V_\mathrm{D}} = \frac{N_\mathrm{2}}{N_\mathrm{1}}\frac{D}{1-D}$$

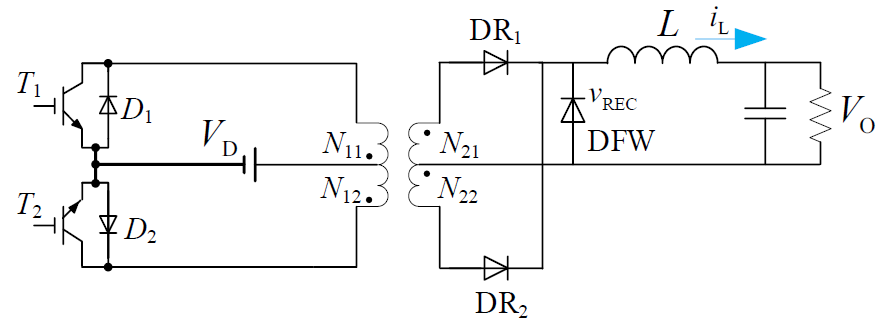
推挽变换器

推挽变换器主要用于低电压高电流的场景。

输入电压与输出电压之间的关系为

$$\frac{V_\mathrm{O}}{V_\mathrm{D}} = 2\frac{N_\mathrm{2}}{N_\mathrm{1}}D$$

第五章 DC-AC 变换器

我们经常按照直流侧储能元件的性质将逆变器分为电压型逆变器 (VSI) 和 电流型逆变器 (CSI)。电压型逆变器的直流侧储能元件为电容，电流型逆变器的直流侧储能元件为电感。VSI 是本章的重点讨论对象。

SPWM 正弦波脉冲宽度调制

SPWM 是用一系列脉宽按照正弦规律变换的脉冲来模拟正弦波。

冲量等效原理

当面积相等而形状不同的短脉冲作用于同一个惯性环节时，其响应基本相同。

SPWM 的工作原理

先引入两个重要的物理量：

调制比 (Amplitude Modulation Ratio, AMR)：

$$m_\mathrm{a} = \frac{\overline{V}_\mathrm{control}}{\overline{V}_\mathrm{tri}}$$

其中，$\overline{V}_\mathrm{control}$ 是调制波的幅值，$\overline{V}_\mathrm{tri}$ 是载波的幅值。

载波比 (Frequency Modulation Ratio, FMR)：

$$m_\mathrm{f} = \frac{f_\mathrm{tri}}{f_1}$$

其中，$f_\mathrm{tri}$ 是载波频率，$f_1$ 是期望输出的正弦波频率。

以单桥臂双极性控制为例，输出电压的基波成分为

$$v_1 = \frac{\overline{V}_\mathrm{control}\sin\omega_1 t}{\overline{V}_\mathrm{tri}}\cdot \frac{V_\mathrm{D}}{2} = m_\mathrm{a}\frac{V_\mathrm{D}}{2}\sin\omega_1 t$$

逆变器的电压增益都等于调制比乘以桥臂电压差，即 $m_\mathrm{a}V$ 。其中，电压差由拓扑决定。

上式只在 $m_\mathrm{a} \leq 1$ 时成立。我们称 $m_\mathrm{a} \leq 1$ 时为线性调制，$m_\mathrm{a} > 1$ 时为过调制。

为了消除偶次谐波，在双极性调制中，我们需要控制 $m_\mathrm{f}$ 为奇数。

同步调制与异步调制

同步调制是指调制波频率变化时，载波频率相应地变化，从而保持载波比 $m_\mathrm{f}$ 不变。
异步调制是指调制波频率变化时，载波频率不变。

同步调制可以有效抑制谐波含量，但是控制相对复杂。为此我们可以使用分段同步调制，将输出频率划分为几个频段，仅保持各个频段内载波比 $m_\mathrm{f}$ 不变。但我们大多还是使用异步调制。

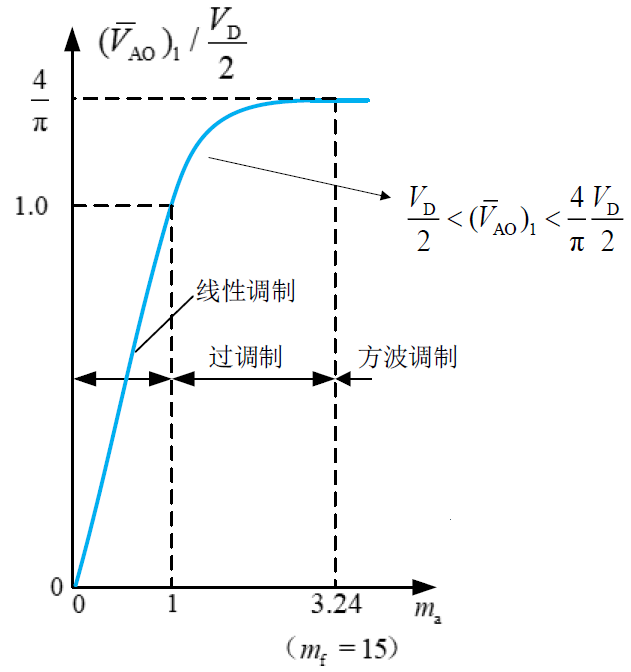
过调制与方波调制

过调制是指调制比 $m_\mathrm{a} > 1$ 的情况，此时输出电压谐波含量更大，一般用于电机驱动中。

如果 $\overline{V}_\mathrm{control} \gg \overline{V}_\mathrm{tri}$ ，则输出电压近似为方波，此时称为方波调制。

具体实现

计算脉宽有两种方法

自然采样法

$$t = \frac{T_\mathrm{s}}{2}\left[1+\frac{m_\mathrm{a}}{2}(\sin\omega t_\mathrm{a}+\sin\omega t_\mathrm{b})\right]$$

规则采样法

$$t = \frac{T_\mathrm{s}}{2}\left(1+m_\mathrm{a}\sin\omega t_\mathrm{d}\right)$$

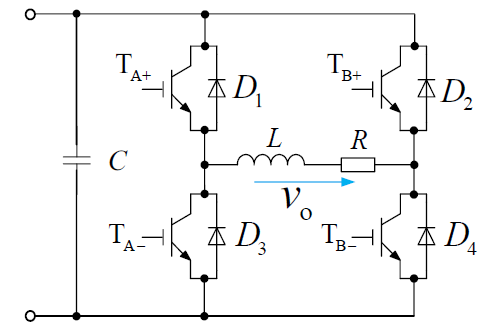
单相逆变器

主要使用单相全桥逆变器，包含三种调制方式。我们只需要记得不同调制方式下，载波比 $m_\mathrm{f}$ 的取值与偶次谐波的抑制关系即可。

调制方式	载波比 $m_\mathrm{f}$	最低次谐波位置
双极性调制	$m_\mathrm{f}$ 取奇数	$m_\mathrm{f}$ 附近（含）
单极性调制	$m_\mathrm{f}$ 取偶数	$m_\mathrm{f}$ 附近（不含）
单极性倍频调制	$m_\mathrm{f}$ 任意	$2m_\mathrm{f}$ 附近（不含）

同样，过调制和方波调制的幅值也为 1 倍和 $\displaystyle\frac{4}{\pi}$ 倍。

三相逆变器

每一个桥臂与单相逆变器分析完全相同。但是由于每一相相差 $120^\circ$ ，所以其线电压线性调制的最大值只有 $\displaystyle\frac{\sqrt{3}}{2}\approx 0.866$ 倍，方波调制的最大值为 1.1 倍。

SVPWM 空间矢量脉宽调制

对一个三相逆变器，每一组桥臂都有上开下关和下开上关两种状态，分别记为 1 和 0。这样就有 $2^3=8$ 种状态，其中 000 和 111 两种状态为空矢量。我们可以将这 8 种状态看做不同的空间矢量，称为空间矢量脉宽调制 (SVPWM)。

通常我们使用 7 段对称调制法，步骤如下：

1. 计算出期望输出电压的空间矢量 $V_\mathrm{d}$ 的幅值和相位角，确定扇区
2. 将 $V_\mathrm{d}$ 分解为两个相邻的矢量 $V_\mathrm{a}$ 和 $V_\mathrm{b}$ 的线性组合
3. 计算 $V_\mathrm{a}$ 和 $V_\mathrm{b}$ 的占空比，确定矢量控制时间 $t_\mathrm{a}$ 和 $t_\mathrm{b}$
4. 计算零矢量的占空比，确定零矢量控制时间 $t_0$
5. 在一个周期内，两侧和中间分别为零矢量 000 和 111，时间为 $\frac{t_0}{4}$；中间为非零矢量开启时间，时间分别为 $\frac{t_\mathrm{a}}{2}$ 和 $\frac{t_\mathrm{b}}{2}$

当然，在上述调制方式外，也有一些其他的调制方法，如选择性谐波消除控制、三次谐波注入控制、滞环电流控制等。

第六章 AC-DC 变换器

本章介绍各种整流电路。我们将会从单相整流电路开始，逐步扩展到三相整流电路；从最简单的阻性负载到复杂的感性、容性负载一步步分析。对于不控整流电路，可以看做是晶闸管整流电路导通角为 0 的特殊情况。

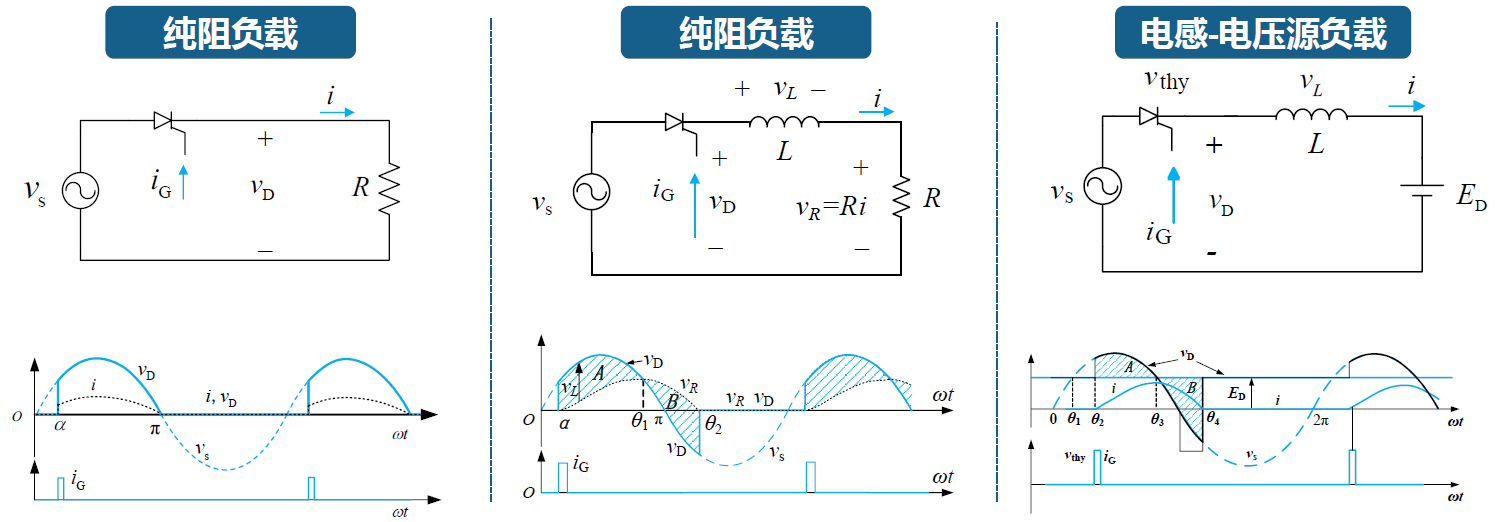
单相半波可控整流电路

阻性负载

如上图所示，晶闸管的导通角 $\alpha$ 可以通过门极电流来控制。假设晶闸管的导通角为 $\alpha$，则输出电压为

$$V_\mathrm{D} = \frac{1}{2\pi}\int_\alpha^{\pi}\sqrt{2}V_\mathrm{s}\sin\omega t\ \mathrm{d}(\omega t) = 0.45V_\mathrm{s}\frac{1+\cos\alpha}{2}$$

单相半波可控整流电路的一个积分周期为 $2\pi$ ，移相范围为 $[0, 180^\circ]$ 。注意，单相逆变器的控制角是从电压 0 点开始计算的，即 $0^\circ$ 。

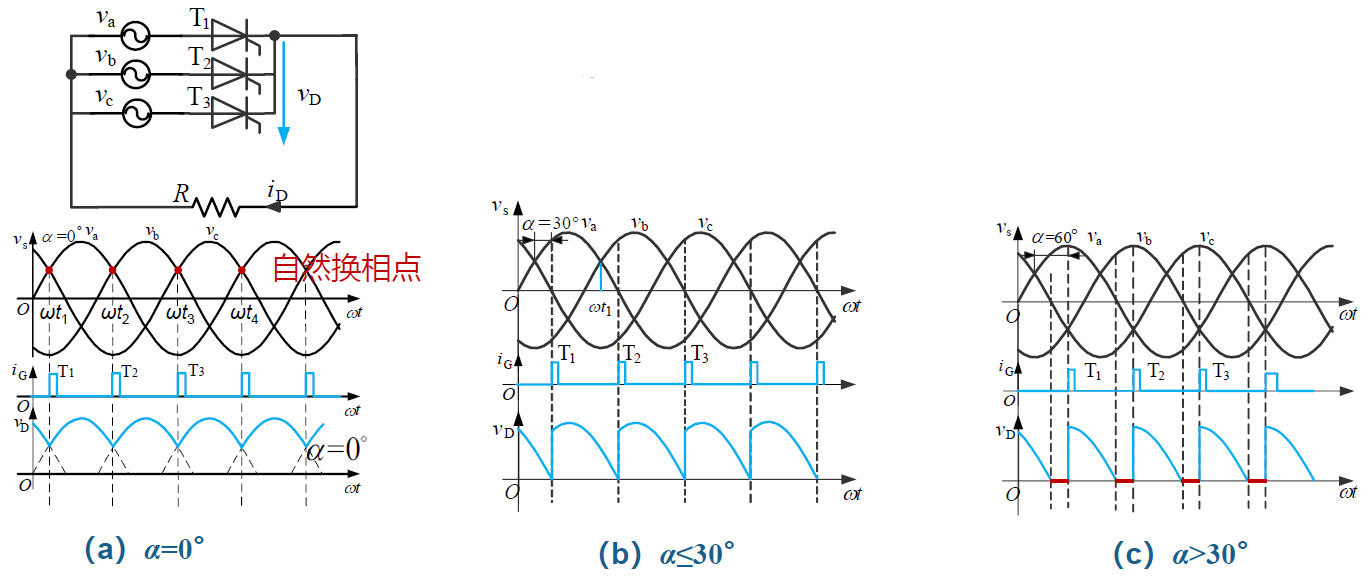
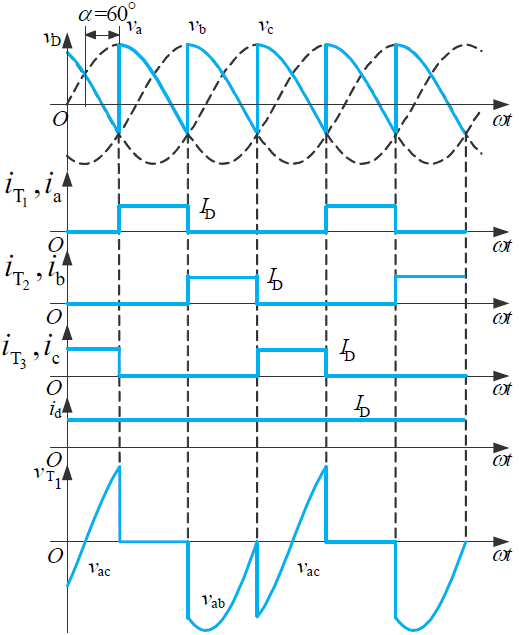
三相半波可控整流电路

阻性负载

在 $\alpha \le 30^\circ$ 时，负载电流连续，输出电压平均值为

$$V_\mathrm{D} = \frac{1}{\frac{2\pi}{3}}\int_{\frac{\pi}{6}+\alpha}^{\frac{5\pi}{6}+\alpha}\sqrt{2}V_\mathrm{s}\sin\omega t\ \mathrm{d}(\omega t) = 1.17V_\mathrm{s}\cos\alpha$$

在 $\alpha > 30^\circ$ 时，负载电流不连续，输出电压平均值为

$$V_\mathrm{D} = \frac{1}{\frac{2\pi}{3}}\int_{\frac{\pi}{6}+\alpha}^{\pi}\sqrt{2}V_\mathrm{s}\sin\omega t\ \mathrm{d}(\omega t) = 0.675V_\mathrm{s}\left[1+\cos\left(\frac{\pi}{6}+\alpha\right)\right]$$

阻感负载

在有电感且电感足够大的情况下，电流一定会连续。这种情况我们都可以把负载看成一个电流源。因此电压平均值的计算公式与阻性负载在 $\alpha \le 30^\circ$ 时相同，即

$$V_\mathrm{D} = 1.17V_\mathrm{s}\cos\alpha$$

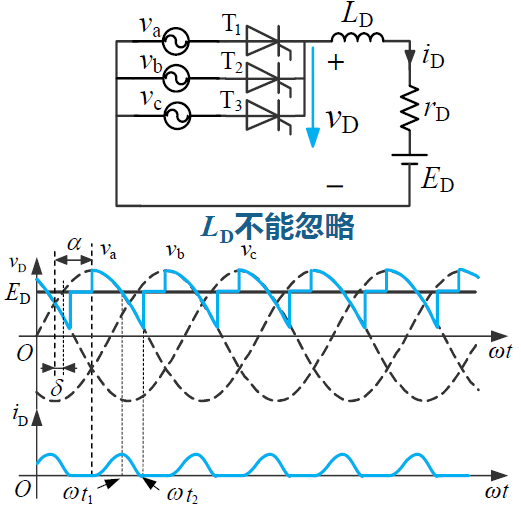
反电动势负载

图中为电感比较小的情况，这时需要用伏秒平衡去分析。但是一般我们认为电感比较大，即电流连续，所以输出电压平均值仍与连续是一致，即

$$V_\mathrm{D} = 1.17V_\mathrm{s}\cos\alpha$$

平均电流为

$$I_\mathrm{D} = \frac{V_\mathrm{D}-E_\mathrm{D}}{r}$$

三相半波可控整流电路触发角为 0 的点为相电压的自然换相点，此时 $\alpha=30^\circ$ ，这与单相时是不一致的。此外，三相半波可控整流电路的一个积分周期为 $\frac{2\pi}{3}$ ，阻性负载移相范围为 $[0, 150^\circ]$，阻感负载移相范围为 $[0, 90^\circ]$ 。

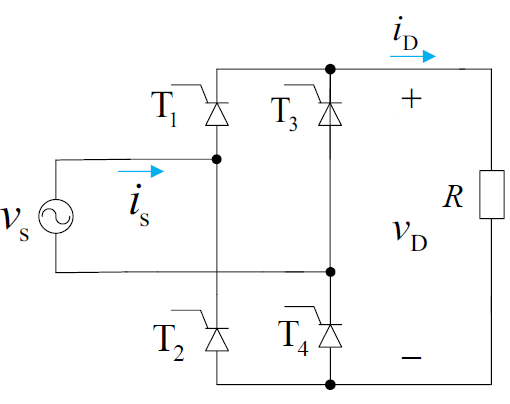
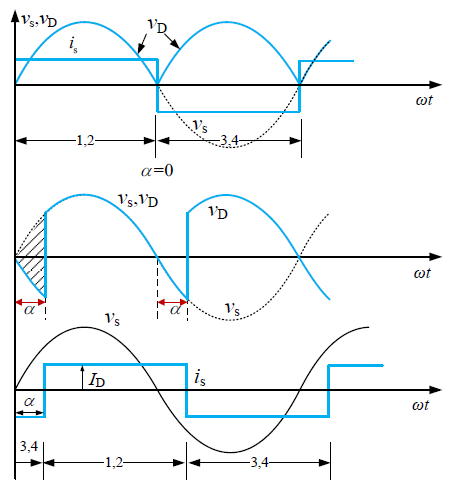
单相桥式可控整流电路

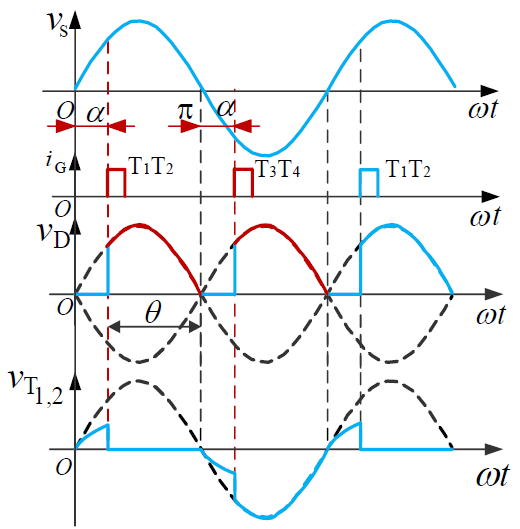
阻性负载

$$V_\mathrm{D} = \frac{1}{\pi}\int_\alpha^{\pi}\sqrt{2}V_\mathrm{s}\sin\omega t\ \mathrm{d}(\omega t) = 0.9V_\mathrm{s}\frac{1+\cos\alpha}{2}$$

阻感负载

在有电感且电感足够大的情况下，电流连续，输出电压平均值为

$$V_\mathrm{D} = \frac{1}{\pi}\int_\alpha^{\pi+\alpha}\sqrt{2}V_\mathrm{s}\sin\omega t\ \mathrm{d}(\omega t) = 0.9V_\mathrm{s}\cos\alpha$$

在不考虑换流过程的情况下，相移功率因数为 $\cos\alpha$ ，畸变因数为 0.9 。

单相桥式可控整流电路的一个积分周期为 $\pi$ ，阻性负载移相范围为 $[0, 180^\circ]$ ，阻感负载移相范围为 $[0, 90^\circ]$。单相逆变器的控制角是从电压 0 点开始计算的，即 $0^\circ$ 。

注意，考试可能有坑。题目会把下桥臂的两个晶闸管换成二极管，变成半控电路。此时要当做阻性负载来看；或者会在阻感负载上并联一个续流二极管，此时也要当做阻性负载来看。

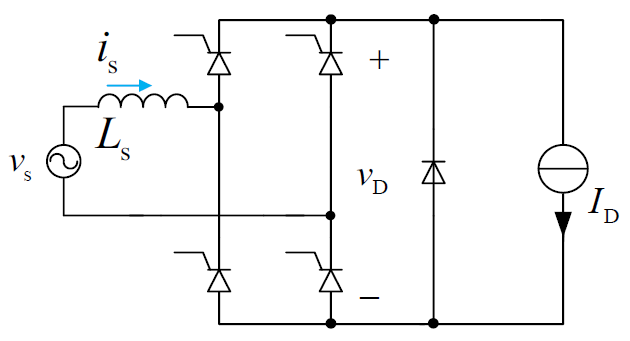
考虑输入电感时的阻感负载

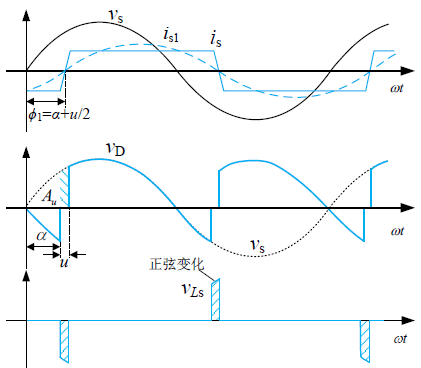
由于存在输入电感，换流过程不再是瞬间完成，这段时间称为换流时间，对应的角度称为换相重叠角，用字母 $u$ 表示。

换流时，用积分计算电压损失面积 $A_u$

$$A_u = \int_\alpha^{\alpha+u}\sqrt{2}V_\mathrm{s}\sin\omega t\ \mathrm{d}(\omega t) = \int_\alpha^{\alpha+u}L_\mathrm{s}\frac{\mathrm{d}i_\mathrm{s}}{\mathrm{d}t}\mathrm{d}(\omega t) = \omega L_\mathrm{s} \int_{-I_\mathrm{D}}^{I_\mathrm{D}}\mathrm{d}i_\mathrm{s}$$

化简得到

$$A_u = \sqrt{2}V_\mathrm{s}[\cos\alpha - \cos(\alpha + u)] = 2\omega L_\mathrm{s} I_\mathrm{D}$$

因此，输出电压平均值为

$$V_\mathrm{D} = 0.9V_\mathrm{s}\cos\alpha - \frac{A_u}{\pi} = 0.9V_\mathrm{s}\cos\alpha - \frac{2\omega L_\mathrm{s} I_\mathrm{D}}{\pi}$$

换相重叠角

$$\cos(\alpha + u) = \cos\alpha - \frac{2\omega L_\mathrm{s} I_\mathrm{D}}{\sqrt{2}V_\mathrm{s}}$$

相移功率因数

$$DPF \approx \cos\left(\alpha + \frac{1}{2}u\right)$$

根据输入输出功率平衡 $V_\mathrm{s}I_\mathrm{s1}DPF=V_\mathrm{D}I_\mathrm{D}$ ，可以得到基波输入电流有效值

$$I_\mathrm{s1} = \frac{V_\mathrm{D}I_\mathrm{D}}{V_\mathrm{s}DPF} = \frac{0.9V_\mathrm{s}\cos\alpha - \frac{2\omega L_\mathrm{s} I_\mathrm{D}}{\pi}}{V_\mathrm{s}\cos\left(\alpha + \frac{1}{2}u\right)}I_\mathrm{D}$$

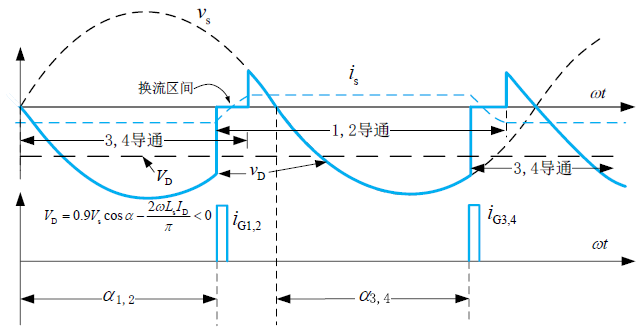
逆变模式

逆变模式需要满足以下条件：

1. 电动势 $E_\mathrm{D}$ 反向
2. 导通角满足 $90^\circ < \alpha < 180^\circ$
3. $|E_\mathrm{D}| > |V_\mathrm{D}|$

定义熄灭角

$$\gamma = \pi - (\alpha + u)$$

逆变角

$$\beta = \pi - \alpha$$

则有

$$\gamma = \beta - u$$

熄灭时间必须要大于晶闸管关断时间，折算成角度 $\theta$ 约为 $5^\circ$ ，再加上一个安全裕量角 $\varphi$ ，则有

$$\gamma > \theta + \varphi$$

即

$$\beta > u + \theta + \varphi$$

启动时，要在满足逆变角最小值的情况下，尽量增大导通角 $\alpha$ 使得电流断续。

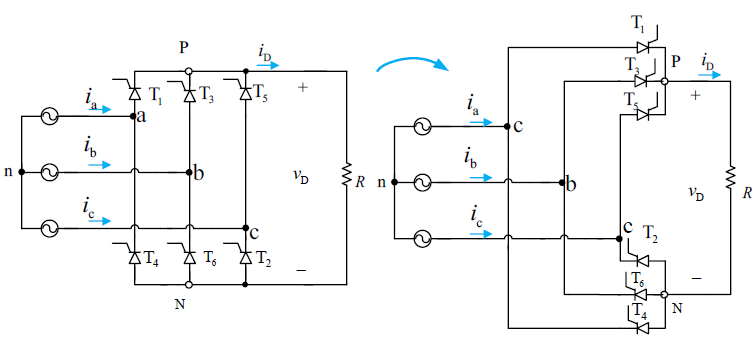
三相桥式可控整流电路

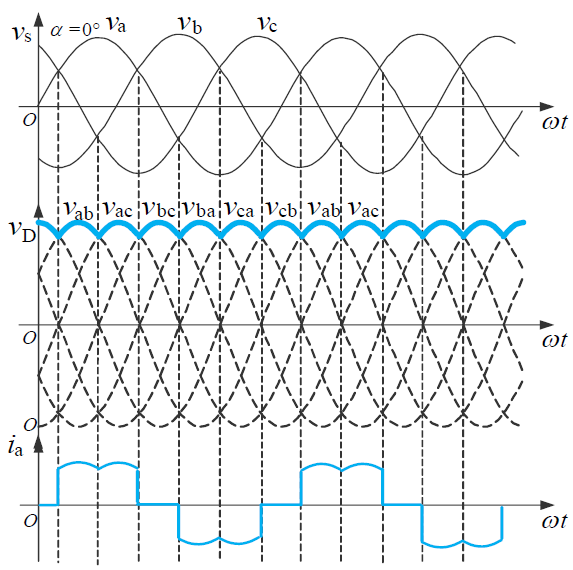
阻性负载

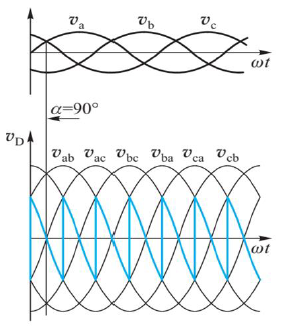
在 $\alpha \le 60^\circ$ 时，负载电流连续，输出电压平均值为

$$V_\mathrm{D} = \frac{1}{\frac{\pi}{3}}\int_{\frac{\pi}{3}+\alpha}^{\frac{2\pi}{3}+\alpha}\sqrt{2}V_\mathrm{LL}\sin\omega t\ \mathrm{d}(\omega t) = 1.35V_\mathrm{LL}\cos\alpha = 2.34V_\mathrm{s}\cos\alpha$$

在 $\alpha > 60^\circ$ 时，负载电流不连续，输出电压平均值为

$$V_\mathrm{D} = \frac{1}{\frac{\pi}{3}}\int_{\frac{\pi}{3}+\alpha}^{\pi}\sqrt{2}V_\mathrm{LL}\sin\omega t\ \mathrm{d}(\omega t) = 1.35V_\mathrm{LL}\left[1+\cos\left(\frac{\pi}{3}+\alpha\right)\right] = 2.34V_\mathrm{s}\left[1+\cos\left(\frac{\pi}{3}+\alpha\right)\right]$$

阻感负载

在有电感且电感足够大的情况下，电流连续，输出电压平均值为

$$V_\mathrm{D} = 1.35V_\mathrm{LL}\cos\alpha = 2.34V_\mathrm{s}\cos\alpha$$

三相桥式可控整流电路的一个积分周期为 $\frac{\pi}{3}$ ，阻性负载移相范围为 $[0, 120^\circ]$ ，阻感负载移相范围为 $[0, 90^\circ]$。注意，三相全桥逆变器的控制角是从线电压的自然换相点开始计算的，即 $60^\circ$ 。

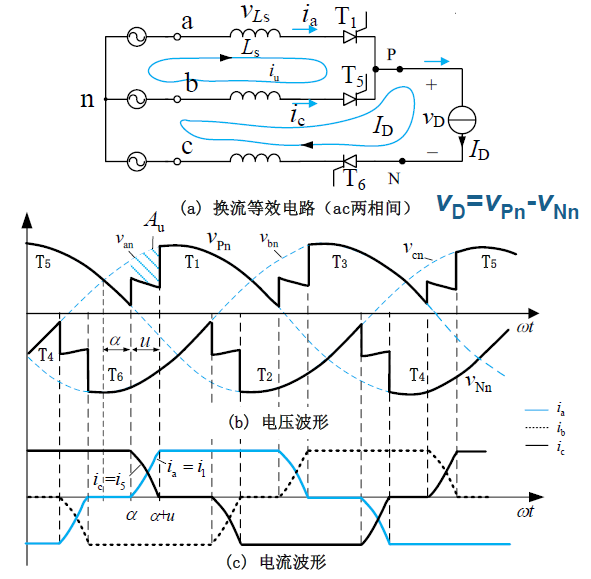
考虑输入电感时的阻感负载

对图中上网孔列网孔方程，得出电压损失为 $\frac{v_\mathrm{ac}}{2}$，则电压损失面积为

$$A_u = \int_\alpha^{\alpha+u}\frac{\sqrt{2}V_\mathrm{LL}}{2}\sin\omega t\ \mathrm{d}(\omega t) = \int_\alpha^{\alpha+u}L_\mathrm{s}\frac{\mathrm{d}i_\mathrm{s}}{\mathrm{d}t}\mathrm{d}(\omega t) = \omega L_\mathrm{s} \int_{0}^{I_\mathrm{D}}\mathrm{d}i_\mathrm{s}$$

化简得到

$$A_u = \frac{\sqrt{2}V_\mathrm{LL}}{2}[\cos\alpha - \cos(\alpha + u)] = \omega L_\mathrm{s} I_\mathrm{D}$$

因此，输出电压平均值为

$$V_\mathrm{D} = 1.35V_\mathrm{LL}\cos\alpha - \frac{A_u}{\frac{\pi}{3}} = 1.35V_\mathrm{LL}\cos\alpha - \frac{3\omega L_\mathrm{s} I_\mathrm{D}}{\pi}$$

换相重叠角

$$\cos(\alpha + u) = \cos\alpha - \frac{2\omega L_\mathrm{s} I_\mathrm{D}}{\sqrt{2}V_\mathrm{LL}}$$

相移功率因数

$$DPF \approx \cos\left(\alpha + \frac{1}{2}u\right)$$

最后，总结一下平均电压、换相压降和换相重叠角的公式：

电路形式	电流连续分界导通角	电流连续时平均电压	电流断续时平均电压	换相压降 $A_u$	换相重叠角$\cos\alpha-\cos(\alpha+u)$	积分周期
单相半波 $m=2$			$0.45V_\mathrm{s}\frac{1+\cos\alpha}{2}$			$2\pi$
三相半波 $m=3$	$30^\circ$	$1.17V_\mathrm{s}\cos\alpha$	$0.675V_\mathrm{s}\left[1+\cos\left(\frac{\pi}{6}+\alpha\right)\right]$	$\frac{3\omega L_\mathrm{s}I_\mathrm{D}}{2\pi}$	$\frac{2\omega L_\mathrm{s}I_\mathrm{D}}{\sqrt{6}V_\mathrm{s}}$	$\frac{2\pi}{3}$
单相桥式 $m=2$		$0.9V_\mathrm{s}\cos\alpha$	$0.9V_\mathrm{s}\frac{1+\cos\alpha}{2}$	$\frac{2\omega L_\mathrm{s}I_\mathrm{D}}{\pi}$	$\frac{2\omega L_\mathrm{s}I_\mathrm{D}}{\sqrt{2}V_\mathrm{s}}$	$\pi$
三相桥式 $m=6$	$60^\circ$	$1.35V_\mathrm{LL}\cos\alpha$	$1.35V_\mathrm{LL}\left[1+\cos\left(\frac{\pi}{3}+\alpha\right)\right]$	$\frac{3\omega L_\mathrm{s}I_\mathrm{D}}{\pi}$	$\frac{2\omega L_\mathrm{s}I_\mathrm{D}}{\sqrt{2}V_\mathrm{LL}}$	$\frac{\pi}{3}$