第一章线路暂态

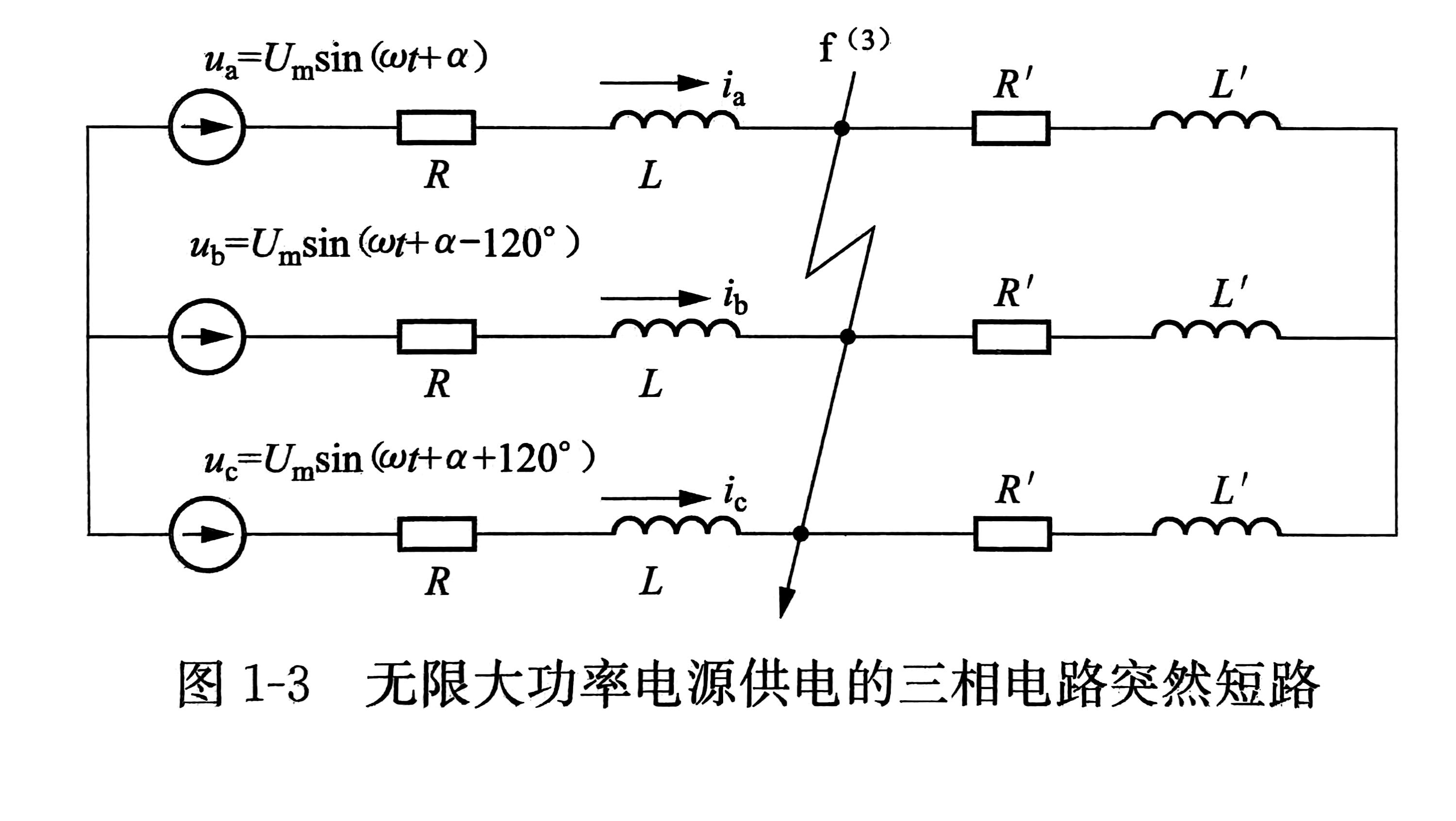
无限大功率电源供电的三相短路电流分析

当电源功率为无穷大时，电源的电压和频率保持恒定，且发电机内阻抗为零。

在这种情况下，短路电流可以使用三要素法计算

$\begin{cases} i_\mathrm{a} = I_\mathrm{m}\sin(\omega t + \alpha -\varphi) + \left[I_\mathrm{m\left|0\right|}\sin(\alpha - \varphi_{\left|0\right|})-I_\mathrm{m}\sin(\alpha-\varphi)\right]\mathrm{e}^{-\frac{t}{T_\mathrm{a}}} \\ \\ i_\mathrm{b} = I_\mathrm{m}\sin(\omega t + \alpha -120^\circ -\varphi) + \left[I_\mathrm{m\left|0\right|}\sin(\alpha-120^\circ - \varphi_{\left|0\right|})-I_\mathrm{m}\sin(\alpha-120^\circ-\varphi)\right]\mathrm{e}^{-\frac{t}{T_\mathrm{a}}} \\ \\ i_\mathrm{c} = I_\mathrm{m}\sin(\omega t + \alpha +120^\circ -\varphi) + \left[I_\mathrm{m\left|0\right|}\sin(\alpha + 120^\circ - \varphi_{\left|0\right|})-I_\mathrm{m}\sin(\alpha + 120^\circ-\varphi)\right]\mathrm{e}^{-\frac{t}{T_\mathrm{a}}} \end{cases}$

其中，$I_\mathrm{m}$ 为稳态短路电流的幅值，$I_\mathrm{m\left|0\right|}$ 为短路前电流的幅值，$\alpha$ 为短路发生时的相位角，$\varphi=\arctan\frac{\omega L}{R}$ 为短路后的阻抗角，$\varphi_{\left|0\right|}=\arctan\frac{\omega (L+L’)}{R+R’}$ 为短路前的阻抗角，$T_\mathrm{a}=\frac{L}{R}$ 为三相短路的时间常数。

三相短路最严重的情况是：在空载条件下短路角满足 $\left|\alpha-\varphi\right|=90^\circ$ ，此时直流分量起始值最大。

短路冲击电流

将 $I_\mathrm{m\left|0\right|}=0$ ，$\varphi=90^\circ$ ，$\alpha=0$ 代入短路电流公式有

$i_\mathrm{a} = -I_\mathrm{m}\cos{\omega t} + I_\mathrm{m}\mathrm{e}^{-\frac{t}{T_\mathrm{a}}}$

上式约在 $t=0.01\mathrm{s}$ 时达到最大值，由此可得冲击电流值为

$i_\mathrm{M}\approx I_\mathrm{m} + I_\mathrm{m}\mathrm{e}^{-\frac{0.01}{T_\mathrm{a}}} = K_\mathrm{M}I_\mathrm{m}$

$K_\mathrm{M}$ 根据情况选择 1.8 或 1.9 。

短路电流最大有效值

对短路电流第一个周期积分即可，这里直接给出结果

$I_\mathrm{M} = \frac{I_\mathrm{m}}{\sqrt{2}}\sqrt{1+2(K_\mathrm{M}-1)^2}$

当 $K_\mathrm{M}=1.8$ 时，$I_\mathrm{M}\approx 1.52\frac{I_\mathrm{m}}{\sqrt{2}}$；当 $K_\mathrm{M}=1.9$ 时，$I_\mathrm{M}\approx 1.62\frac{I_\mathrm{m}}{\sqrt{2}}$。

第二章机电暂态

机电暂态的产生原因是磁链守恒。在短路时，电流突然变化，但是磁链不能立即变化，因此会阻碍电流的变化。

同步电机稳态运行情况

在此后的讨论中，我们将对同步电机做出以下假设：

同步电机是理想电机
只考虑电磁暂态过程，不考虑线路暂态过程
忽略磁路饱和的影响
短路后不考虑强励，励磁电压不变

正方向定义

转子逆时针旋转为正方向，q 轴超前 d 轴 $90^\circ$ 。选定定子各绕组轴线（即图中 a, b, c 轴）作为各相绕组磁链的正方向。定子电流产生负磁通，转子电流产生正磁通。这样运行时，发电机处于过励状态，电枢反应是去磁的。

同步电机电压平衡关系

其实这一部分电机学已经学过，这里只补充一些内容。

发电机端电压 $u_\mathrm{q}$ 、 $u_\mathrm{d}$ 满足

$u_\mathrm{q} = E_\mathrm{q} - i_\mathrm{d}x_\mathrm{d} \qquad u_\mathrm{d}=i_\mathrm{q}x_\mathrm{q}$

或写成相量形式

$\dot{U}_\mathrm{q} = \dot{E}_\mathrm{q} - \mathrm{j}\dot{I}_\mathrm{d}x_\mathrm{d} \qquad \dot{U}_\mathrm{d} = -\mathrm{j}\dot{I}_\mathrm{q}x_\mathrm{q}$

其中，$x_\mathrm{d}=x_\mathrm{ad}+x_\mathrm{\sigma}$ 称为直轴同步电抗，是由直轴电枢反应电抗和漏电抗组成的。同理，$x_\mathrm{q}=x_\mathrm{aq}+x_\mathrm{\sigma}$ 称为交轴同步电抗。

对于励磁绕组，磁链路径与直轴相同，励磁电抗满足 $x_\mathrm{f}=x_\mathrm{ad}+x_\mathrm{f\sigma}$ 。
在暂态分析中，我们一概不考虑同步电机的机端电阻。

对于隐极机，电压平衡方程为

$\dot{E}_\mathrm{q} = \dot{U} + \mathrm{j}\dot{I}x_\mathrm{d}$

对于凸极机，电压平衡方程为

$\begin{align*} \dot{E}_\mathrm{q} &= \dot{U} + \mathrm{j}\dot{I}_\mathrm{d}x_\mathrm{d} + \mathrm{j}\dot{I}_\mathrm{q}x_\mathrm{q} \\ &= \dot{U} + \mathrm{j}\dot{I}x_\mathrm{q} + \mathrm{j}\dot{I}_\mathrm{d}(x_\mathrm{d}-x_\mathrm{q})\\ &= \dot{E}_{\scriptscriptstyle\mathrm{Q}} + \mathrm{j}\dot{I}_\mathrm{d}(x_\mathrm{d}-x_\mathrm{q}) \end{align*}$

其中，$\dot{E}_{\scriptscriptstyle\mathrm{Q}}$ 为虚拟电动势，用于确定交轴的位置。

同步电机电抗参数和电动势平衡方程

正常运行

$\begin{cases} x_\mathrm{d} = x_\mathrm{\sigma} + x_\mathrm{ad} \\ \\ x_\mathrm{q} = x_\mathrm{\sigma} + x_\mathrm{aq} \\ \\ x_\mathrm{f} = x_\mathrm{f\sigma} + x_\mathrm{ad} \\ \\ \dot{E}_\mathrm{q} = \dot{U}_\mathrm{q} + \mathrm{j}\dot{I}_\mathrm{d}x_\mathrm{d} \end{cases}$

励磁电抗也加了直轴电枢反应电抗，是因为二者磁路是一致的。

暂态参数（忽略阻尼绕组）

$\begin{cases} x_\mathrm{d}' = x_\mathrm{\sigma} + \displaystyle\frac{1}{\frac{1}{x_\mathrm{ad}}+\frac{1}{x_\mathrm{f\sigma}}} \\ \\ x_\mathrm{q}' = x_\mathrm{q} \\ \\ \dot{E}_\mathrm{q}' = \dot{U}_\mathrm{q} + \mathrm{j}\dot{I}_\mathrm{d}x_\mathrm{d}' \end{cases}$

q 轴暂态电抗 $x_\mathrm{q}’$ 与稳态相同，因为 q 轴电抗不受励磁绕组的影响。

次暂态参数（考虑阻尼绕组）

$\begin{cases} x_\mathrm{d}'' = x_\mathrm{\sigma} + \displaystyle\frac{1}{\frac{1}{x_\mathrm{ad}}+\frac{1}{x_\mathrm{f\sigma}}+\frac{1}{x_\mathrm{D\sigma}}} \\ \\ x_\mathrm{q}'' = x_\mathrm{q} + \displaystyle\frac{1}{\frac{1}{x_\mathrm{aq}}+\frac{1}{x_\mathrm{Q\sigma}}} \\ \\ \dot{E}_\mathrm{q}'' = \dot{U}_\mathrm{q} + \mathrm{j}\dot{I}_\mathrm{d}x_\mathrm{d}''\\ \\ \dot{E}_\mathrm{d}'' = \dot{U}_\mathrm{d} + \mathrm{j}\dot{I}_\mathrm{q}x_\mathrm{q}'' \end{cases}$

短路电流基频交流分量的初始值和稳态有效值

稳态值

q 轴分量为 0 （只有电抗），d 轴分量为

$I_\mathrm{d} = \frac{E_\mathrm{q}}{x_\mathrm{d}}$

暂态和次暂态初始值

$I_\mathrm{d}' = \frac{E_\mathrm{q}'}{x_\mathrm{d}'} \qquad I_\mathrm{d}'' = \frac{E_\mathrm{q}''}{x_\mathrm{d}''} \qquad I_\mathrm{q}'' = \frac{E_\mathrm{d}''}{x_\mathrm{q}''}$

Park 变换

Park 变换是将三相交流电压或电流转换为直流电压或电流的变换方法。复杂的交变电感应可以通过 Park 变换简化。

Park 矩阵为

$\mathbf{P} = \frac{2}{3} \begin{bmatrix} \cos\theta & \cos(\theta-120^\circ) & \cos(\theta+120^\circ) \\ -\sin\theta & -\sin(\theta-120^\circ) & -\sin(\theta+120^\circ) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{bmatrix}$

其逆矩阵为

$\mathbf{P}^{-1} = \begin{bmatrix} \cos\theta & -\sin\theta & 1 \\ \cos(\theta-120^\circ) & -\sin(\theta-120^\circ) & 1 \\ \cos(\theta+120^\circ) & -\sin(\theta+120^\circ) & 1 \end{bmatrix}$

经过 Park 变换后，我们可以得到同步电机电压方程和磁链方程

$\begin{bmatrix} u_\mathrm{d} \\ u_\mathrm{q} \\ u_\mathrm{0} \\ u_\mathrm{f} \\ u_{\scriptscriptstyle\mathrm{D}} \\ u_{\scriptscriptstyle\mathrm{Q}} \end{bmatrix}=\begin{bmatrix} r & & & & & \\ & r & & & & \\ & & r & & & \\ & & & r_\mathrm{f} & & \\ & & & & r_{\scriptscriptstyle\mathrm{D}} & \\ & & & & & r_{\scriptscriptstyle\mathrm{Q}} \end{bmatrix}\begin{bmatrix} -i_\mathrm{d} \\ -i_\mathrm{q} \\ -i_\mathrm{0} \\ i_\mathrm{f} \\ i_{\scriptscriptstyle\mathrm{D}} \\ i_{\scriptscriptstyle\mathrm{Q}} \end{bmatrix}+\begin{bmatrix} \dot{\psi}_\mathrm{d} \\ \dot{\psi}_\mathrm{q} \\ \dot{\psi}_\mathrm{0} \\ \dot{\psi}_\mathrm{f} \\ \dot{\psi}_{\scriptscriptstyle\mathrm{D}} \\ \dot{\psi}_{\scriptscriptstyle\mathrm{Q}} \end{bmatrix} -\begin{bmatrix} \omega \psi_\mathrm{q} \\ \omega \psi_\mathrm{d} \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}$ $\begin{bmatrix} \psi_\mathrm{d} \\ \psi_\mathrm{q} \\ \psi_\mathrm{0} \\ \psi_\mathrm{f} \\ \psi_{\scriptscriptstyle\mathrm{D}} \\ \psi_{\scriptscriptstyle\mathrm{Q}} \end{bmatrix}= \begin{bmatrix} x_\mathrm{d} & & & x_\mathrm{ad} & x_\mathrm{ad} & \\ & x_\mathrm{q} & & & & x_\mathrm{aq}\\ & & x_\mathrm{0} & & & \\ x_\mathrm{ad} & & & x_\mathrm{f} & x_\mathrm{ad} & \\ x_\mathrm{ad} & & & x_\mathrm{ad} & x_{\scriptscriptstyle\mathrm{D}} & \\ & x_\mathrm{aq} & & & & x_{\scriptscriptstyle\mathrm{Q}} \end{bmatrix} \begin{bmatrix} -i_\mathrm{d} \\ -i_\mathrm{q} \\ -i_\mathrm{0} \\ i_\mathrm{f} \\ i_{\scriptscriptstyle\mathrm{D}} \\ i_{\scriptscriptstyle\mathrm{Q}} \end{bmatrix}$

这两个矩阵就是同步电机基本方程。

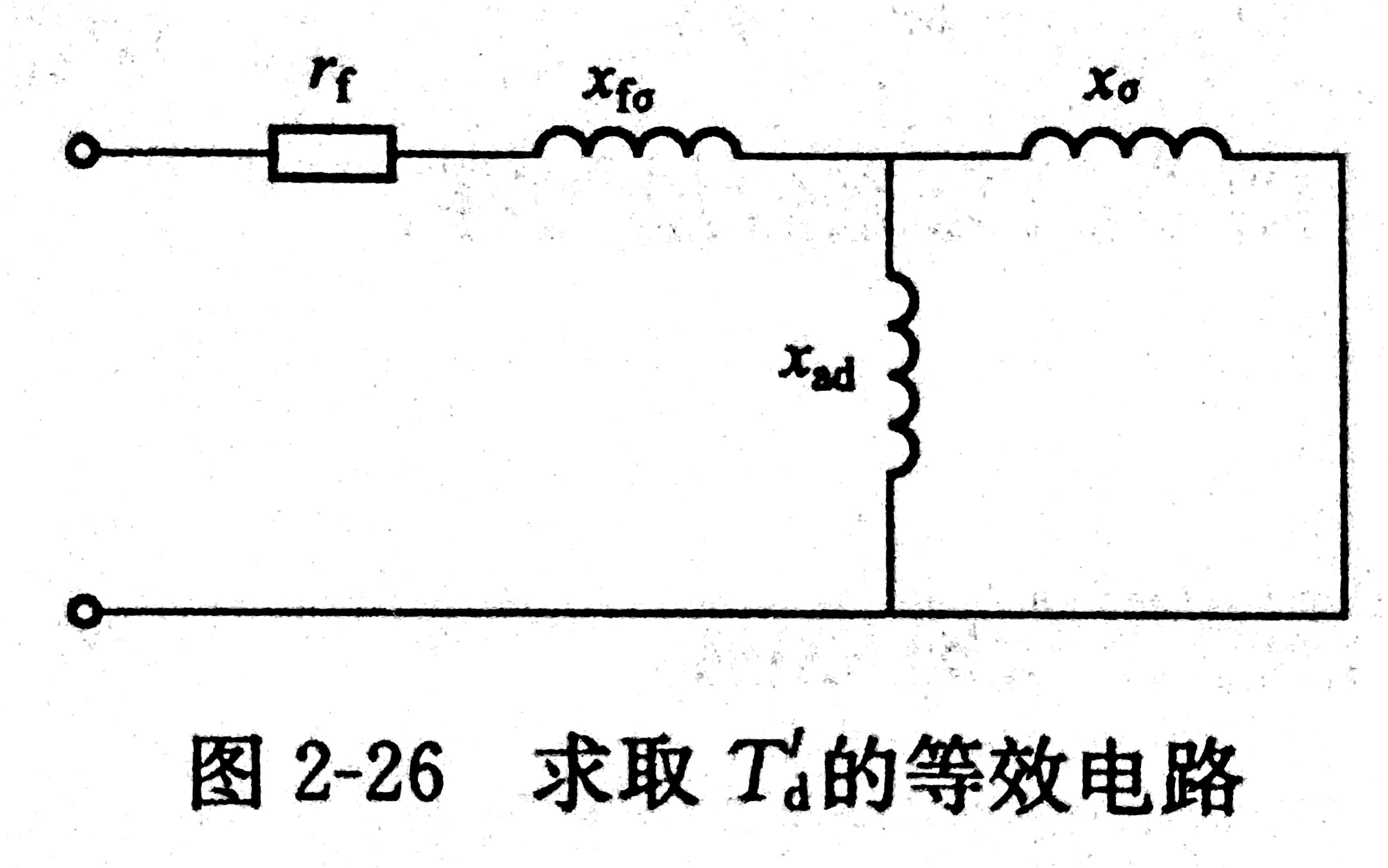
全电流各分量时间常数

忽略阻尼绕组

$\begin{cases} T_\mathrm{f}=\displaystyle\frac{x_\mathrm{f}}{2\pi f r_\mathrm{f}} \\ \\ T_\mathrm{d}'=\displaystyle\frac{x_\mathrm{d}'}{x_\mathrm{d}}T_\mathrm{f} \\ \\ T_\mathrm{a}=\displaystyle\frac{2x_\mathrm{d}'x_\mathrm{q}'}{2\pi f r(x_\mathrm{d}'+x_\mathrm{q}')} \end{cases}$

第一个式子很容易理解，这就是励磁回路的时间常数。

第二个式子可以画出等效电路，其决定了定子中基频暂态分量的衰减。

第三个式子是定子回路的时间常数，决定了转子中基频暂态分量和定子中倍频分量的衰减。

考虑阻尼绕组

$T_\mathrm{d}'=T_\mathrm{f}'=\displaystyle\frac{x_\mathrm{d}'}{x_\mathrm{d}}T_\mathrm{f}$ $T_{\scriptscriptstyle\mathrm{D}}=\displaystyle\frac{x_{\scriptscriptstyle\mathrm{D}}}{2\pi f r_{\scriptscriptstyle\mathrm{D}}} \qquad T_{\scriptscriptstyle\mathrm{Q}}=\displaystyle\frac{x_{\scriptscriptstyle\mathrm{Q}}}{2\pi f r_{\scriptscriptstyle\mathrm{Q}}}$ $x_{\scriptscriptstyle\mathrm{D}}'=x_\mathrm{D\sigma}+\frac{x_\sigma x_\mathrm{ad}}{x_\mathrm{ad}+x_\mathrm{\sigma}}=x_\mathrm{D\sigma}+x_\mathrm{ad}' \qquad x_\mathrm{f}'=x_\mathrm{f\sigma}+\frac{x_\sigma x_\mathrm{ad}}{x_\mathrm{ad}+x_\mathrm{\sigma}}=x_\mathrm{f\sigma}+x_\mathrm{ad}'$ $T_{\scriptscriptstyle\mathrm{D}}''=\left(1-\frac{x_\mathrm{ad}'^2}{x_{\scriptscriptstyle\mathrm{D}}'x_\mathrm{f}'}\right)T_{\scriptscriptstyle\mathrm{D}}'$ $T_\mathrm{a}=\displaystyle\frac{2x_\mathrm{d}''x_\mathrm{q}''}{2\pi f r(x_\mathrm{d}''+x_\mathrm{q}'')}$ $T_\mathrm{q}''=T_{\scriptscriptstyle\mathrm{Q}}\displaystyle\frac{x_\mathrm{q}''}{x_\mathrm{q}}$

电流分量对应关系

直流分量的衰减决定了其他交流分量的衰减。

电动势的产生

稳态交轴电动势

从同步电机基本方程中，我们可以得到

$E_\mathrm{q} = x_\mathrm{ad}i_\mathrm{f}$

暂态交轴电动势

$E_\mathrm{q}' = \frac{x_\mathrm{ad}}{x_\mathrm{f}}\psi_\mathrm{f}$

次暂态交轴电动势和直轴电动势

$E_\mathrm{q}'' = \frac{\frac{\psi_\mathrm{f}}{x_\mathrm{f\sigma}}+\frac{\psi_{\scriptscriptstyle\mathrm{D}}}{x_\mathrm{D\sigma}}}{\frac{1}{x_\mathrm{ad}}+\frac{1}{x_\mathrm{f\sigma}}+\frac{1}{x_\mathrm{D\sigma}}} \qquad E_\mathrm{d}'' = -\frac{x_\mathrm{aq}}{x_{\scriptscriptstyle\mathrm{Q}}}\psi_{\scriptscriptstyle\mathrm{Q}}$

所以，当题目问你，哪些电动势在短路时会突变，我们就可以知道：正比于电流的会突变，正比于磁链的不会突变。

第三章电机转子运动方程和机电特性

转子运动方程

根据转动力学，转子的机械角速度与转矩有如下关系

$J\frac{\mathrm{d}\Omega}{\mathrm{d}t} = M_\mathrm{T} - M_\mathrm{E}$

其中，$M_\mathrm{T}$ 为转子机械转矩，$M_\mathrm{E}$ 为电磁转矩，$J$ 为转动惯量。

在额定转速下，转子的动能为

$W_\mathrm{k}=\frac{1}{2}J\Omega_0^2$

代入转子运动方程，得到

$\frac{2W_\mathrm{k}}{\Omega_0^2}\frac{\mathrm{d}\Omega}{\mathrm{d}t} = \Delta M$

采用标幺制，两边同时除以转矩基准值 $ M_\mathrm{B}=\displaystyle\frac{S_\mathrm{B}}{\Omega_0}$ ，得到

$\frac{2W_\mathrm{k}}{S_\mathrm{B}\Omega_0}\frac{\mathrm{d}\Omega}{\mathrm{d}t} = \frac{2W_\mathrm{k}}{S_\mathrm{B}\omega_0}\frac{\mathrm{d}\omega}{\mathrm{d}t} = \Delta M_*$

记惯性时间常数 $T_\mathrm{J}=\displaystyle\frac{2W_\mathrm{k}}{S_\mathrm{B}}$ ，则有

$\frac{T_\mathrm{J}}{\omega_0}\frac{\mathrm{d}\omega}{\mathrm{d}t} = T_\mathrm{J}\frac{\mathrm{d}\omega_*}{\mathrm{d}t} = \Delta M_*$

在正常工作状态下，机械角速度近似为额定转速，即 $ \Omega_* \approx 1$ ，因此转矩的标幺值等于功率的标幺值，则有

$T_\mathrm{J}\frac{\mathrm{d}\omega_*}{\mathrm{d}t} = p_\mathrm{T*} - p_\mathrm{E*}$

惯性时间常数的物理意义为，在转子上加上额定转矩，转子从静止状态匀加速到额定转速所需的时间。也可以改写为

$T_\mathrm{J} = \frac{2.74GD^2}{10^6 S_\mathrm{B}}n^2$

其中，$GD$ 为转子飞轮矩（$\mathrm{t}\cdot \mathrm{m}^2$ ，这与电机控制技术的飞轮矩不一样！），$n$ 为转速(rpm)，$S_\mathrm{B}$ 为额定容量(MVA)。

功角与电角速度之间有

$\frac{\mathrm{d}\delta}{\mathrm{d}t} = \omega - \omega_0 = \omega_0(\omega_*-1)$

这样，我们就得到了转子运动方程的完整形式

$\begin{cases} T_\mathrm{J}\displaystyle\frac{\mathrm{d}\omega_*}{\mathrm{d}t} = p_\mathrm{T*} - p_\mathrm{E*} \\ \\ \displaystyle\frac{\mathrm{d}\delta}{\mathrm{d}t} = \omega - \omega_0 = \omega_0(\omega_*-1) \end{cases}$

同步电机机电特性

在稳态条件下，电磁功率满足

$P_\mathrm{E} = U_\mathrm{d}I_\mathrm{d} + U_\mathrm{q}I_\mathrm{q}$

电动势满足

$\begin{cases} E_\mathrm{q} = U_\mathrm{q} + I_\mathrm{d}x_\mathrm{d\Sigma} \\ \\ 0 = U_\mathrm{d} - I_\mathrm{q}x_\mathrm{q\Sigma} \end{cases}$

将电动势代入电磁功率公式，得到

$P_\mathrm{E} = \frac{E_\mathrm{q}U}{x_\mathrm{d\Sigma}}\sin\delta + \frac{U^2}{2}\left(\frac{1}{x_\mathrm{q\Sigma}} - \frac{1}{x_\mathrm{d\Sigma}} \right)\sin{2\delta}$

如果是隐极机，$ x_\mathrm{d\Sigma}=x_\mathrm{q\Sigma} $，就没有第二项。

同样，我们也可以用暂态电动势和暂态电抗表示电磁功率，推导过程一致，得

$P_\mathrm{E} = \frac{E_\mathrm{q}'U}{x_\mathrm{d\Sigma}'}\sin\delta + \frac{U^2}{2}\left(\frac{1}{x_\mathrm{q\Sigma}'} - \frac{1}{x_\mathrm{d\Sigma}'} \right)\sin{2\delta}$

但是后面带的一项会影响计算，所以我们会用 $x_\mathrm{d}’$ 后电动势 $E’$ 来表示电磁功率

$P_\mathrm{E'} = \frac{E'U}{x_\mathrm{d\Sigma}'}\sin\delta'$

其中，$\delta’$ 为 $E’$ 和 $U$ 的相位差。

也可以用机端电压表示电磁功率

$P_\mathrm{U_\mathrm{G}} = \frac{U_\mathrm{G}U}{x_\mathrm{e}}\sin\delta_{\scriptscriptstyle\mathrm{G}}$

由 $E_\mathrm{q}$, $E’$ 和 $U_\mathrm{G}$ 与系统之间的联系电抗满足 $x_\mathrm{d\Sigma} > x_\mathrm{d\Sigma}’ > x_\mathrm{e}$ ，因此它们的功率极限由小到大。

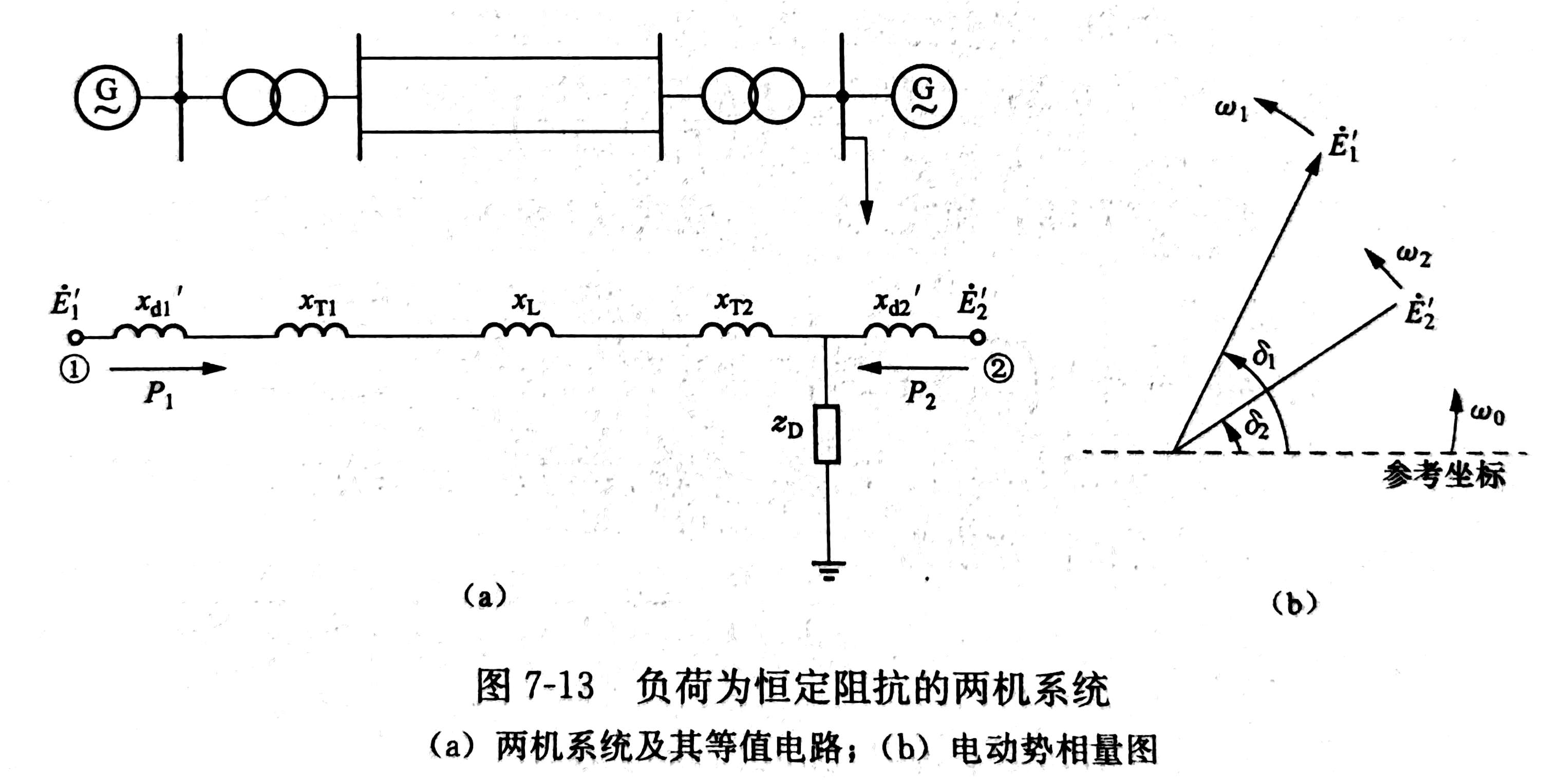
两机系统电磁功率

直接上公式

$\begin{cases} P_\mathrm{E1} = E_1^2 G_{11}+ E_1E_2|Y_{12}|\sin(\delta_{12}+\beta_{12}) \\ \\ P_\mathrm{E2} = E_2^2 G_{22}- E_1E_2|Y_{12}|\sin(\delta_{12}-\beta_{12}) \end{cases}$

其中，$\beta_{12}=\arctan\frac{G_{12}}{B_{12}}$ 。

第四章电力系统小干扰分析

平衡的充要条件与静态稳定储备系数

平衡的充要条件是

$\frac{\mathrm{d}P_\mathrm{E}}{\mathrm{d}\delta} > 0$

静态稳定储备系数定义为

$K_\mathrm{P} = \frac{P_\mathrm{M}-P_0}{P_0} \times 100\%$

小干扰法分析简单系统静态稳定

我们已经求得了转子的运动方程

$\begin{cases} \dot{\omega} = \displaystyle\frac{1}{T_\mathrm{J}} (P_\mathrm{T} - P_\mathrm{E}) \\ \\ \dot{\delta} = \omega_0(\omega-1) \end{cases}$

代入电磁功率表达式，并在平衡点求线性化有

$\begin{bmatrix} \Delta\dot{\delta} \\ \Delta\dot{\omega} \end{bmatrix}= \begin{bmatrix} 0 & \omega_0 \\ -\displaystyle\frac{1}{T_\mathrm{J}}\frac{E_\mathrm{q}U}{x_\mathrm{d\Sigma}}\cos\delta & 0 \end{bmatrix} \begin{bmatrix} \Delta\delta \\ \Delta\omega \end{bmatrix}$

整步功率系数为

$S_\mathrm{Eq} = \frac{E_\mathrm{q}U}{x_\mathrm{d\Sigma}}\cos\delta$

用于判断稳定性。

解出矩阵的特征值

$\rho^2 + \displaystyle\frac{\omega_0}{T_\mathrm{J}}S_\mathrm{Eq} = 0$

得到

$\rho = \pm \sqrt{-\frac{\omega_0}{T_\mathrm{J}}S_\mathrm{Eq}}$

在稳定状态下，比整步功率系数大于 0，因此特征值一定为一对实部为零的共轭复根，即振荡频率

$f=\frac{1}{2\pi}\sqrt{\frac{\omega_0}{T_\mathrm{J}}S_\mathrm{Eq}}$

有阻尼时分析简单系统静态稳定

如果考虑阻尼绕组，则转子运动方程为

$\begin{cases} \dot{\omega} = \displaystyle\frac{1}{T_\mathrm{J}} (P_\mathrm{T} - P_\mathrm{E} - D\omega) \\ \\ \dot{\delta} = \omega_0(\omega-1) \end{cases}$

代入电磁功率表达式，并在平衡点求线性化有

$\begin{bmatrix} \Delta\dot{\delta} \\ \Delta\dot{\omega} \end{bmatrix}= \begin{bmatrix} 0 & \omega_0 \\ -\displaystyle\frac{1}{T_\mathrm{J}}\frac{E_\mathrm{q}U}{x_\mathrm{d\Sigma}}\cos\delta & -\displaystyle\frac{D}{T_\mathrm{J}} \end{bmatrix} \begin{bmatrix} \Delta\delta \\ \Delta\omega \end{bmatrix}$

再次求特征值

$\rho^2 + \frac{D}{T_\mathrm{J}}\rho + \frac{\omega_0}{T_\mathrm{J}}S_\mathrm{Eq} = 0$

得到

$\rho = -\frac{D}{2T_\mathrm{J}} \pm \frac{1}{2T_\mathrm{J}}\sqrt{D^2 - 4T_\mathrm{J}\omega_0 S_\mathrm{Eq}}$

若 $ S_\mathrm{Eq} < 0 $，则无论 $D$ 的大小，总有一个实部为正的特征值，系统将单调地失去稳定性。
若 $ S_\mathrm{Eq} > 0 $，则有两种情况：
- 若 $ D > 0 $，由于 $D$ 值一般不是很大，则特征值为一对实部为负的共轭复根，系统稳定。
- 若 $ D < 0 $，则特征值为一对实部为正的共轭复根，系统振荡失稳。

多机系统的静态稳定近似分析

多机系统过于复杂，我们以两机系统为例。

直接给结论，系统稳定时，两机的功角差 $\delta_{12}$ 满足

$\frac{S_\mathrm{E1}}{T_\mathrm{J1}} - \frac{S_\mathrm{E2}}{T_\mathrm{J2}} > 0$

通常，我们近似地把送端发电机的功率极限作为整个系统的功率极限。

提高静态稳定性的措施

采用自动励磁调节器
减小元件的电抗
- 采用分裂导线
- 提高线路额定电压等级
- 采用串联电容补偿
改善系统的结构
- 增加输电线路回路数
- 增加中间电力系统
采用中间补偿设备

第五章电力系统暂态稳定

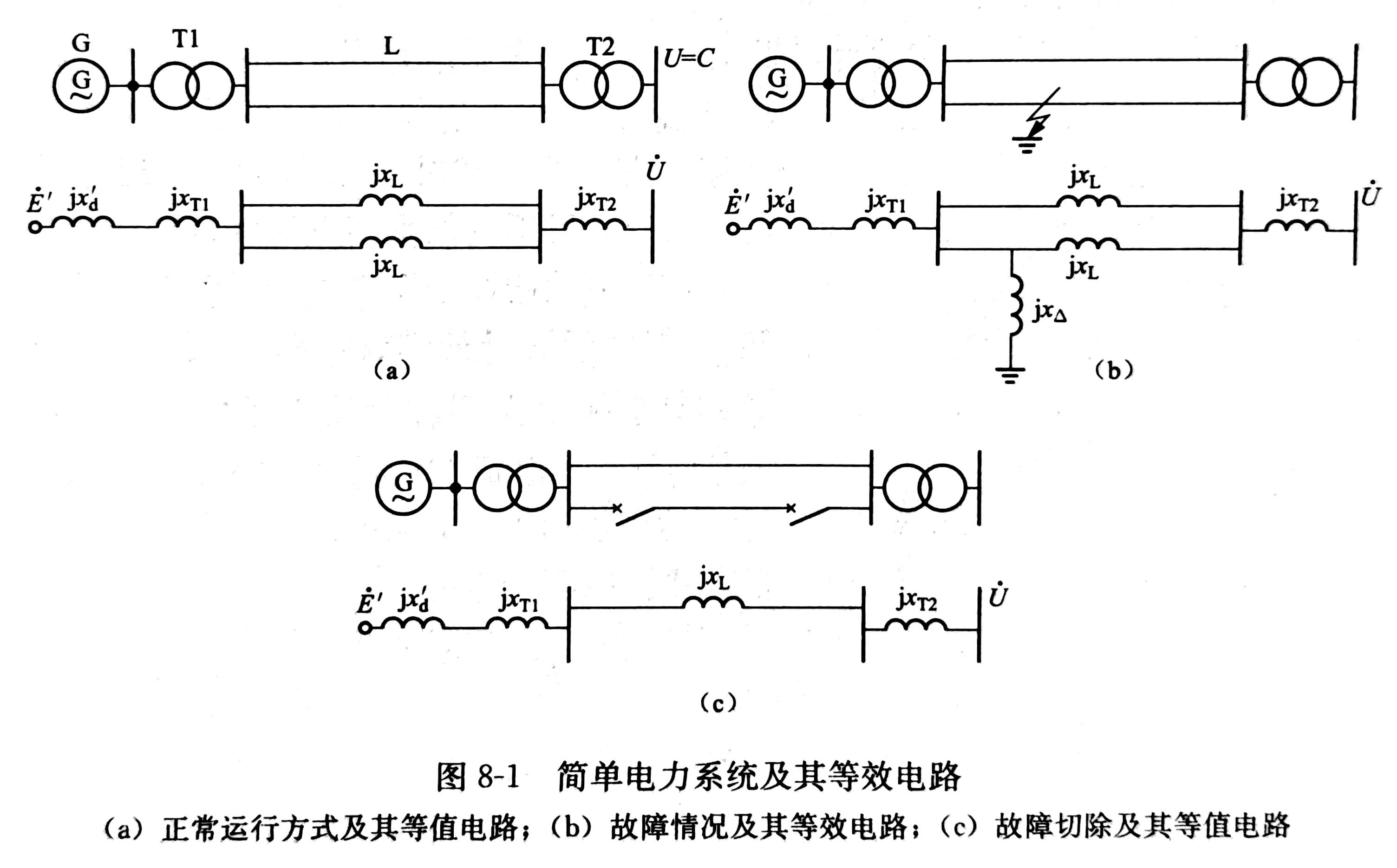
简单系统的稳定性

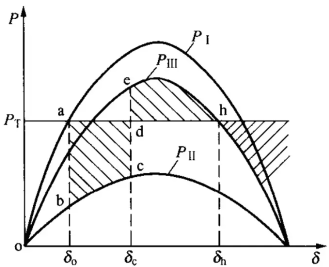
在分析暂态稳定时，我们将整个过程分为三部分：故障前，故障时和故障后。下图为简单电力系统的暂态稳定分析示意图。

故障前

如果发电机以 $\dot{E}’$ 作为等值电动势，则电动势与无穷大系统之间的电抗为

$x_{\scriptscriptstyle\mathrm{I}} = x_\mathrm{d}' + x_{\scriptscriptstyle\mathrm{T1}} + \frac{x_{\scriptscriptstyle\mathrm{L}}}{2} + x_{\scriptscriptstyle\mathrm{T2}}$

电磁功率为

$P_\mathrm{I} = \frac{E'U}{x_{\scriptscriptstyle\mathrm{I}}}\sin\delta$

故障时

根据正序等效定则，只需要在故障点接上一个附加电抗 $x_\Delta$ 即形成正序增广网络。

我们可以用星三角变换转换成三角形网络，电动势与无穷大系统之间的电抗为

$x_{\scriptscriptstyle\mathrm{II}} = (x_\mathrm{d}' + x_{\scriptscriptstyle\mathrm{T1}}) + (\frac{x_{\scriptscriptstyle\mathrm{L}}}{2} + x_{\scriptscriptstyle\mathrm{T2}})+ \frac{(x_\mathrm{d}' + x_{\scriptscriptstyle\mathrm{T1}})(\frac{x_{\scriptscriptstyle\mathrm{L}}}{2} + x_{\scriptscriptstyle\mathrm{T2}})}{x_\Delta}$

同样，电磁功率为

$P_\mathrm{II} = \frac{E'U}{x_{\scriptscriptstyle\mathrm{II}}}\sin\delta$

如果是三相短路，那么发电机和系统之间的联系就被切断了，电磁功率为 0.

故障后

此时，继电保护系统切断了故障线路。

电动势与无穷大系统之间的电抗为

$x_{\scriptscriptstyle\mathrm{III}} = x_\mathrm{d}' + x_{\scriptscriptstyle\mathrm{T1}} + x_{\scriptscriptstyle\mathrm{L}} + x_{\scriptscriptstyle\mathrm{T2}}$